rapidly becomes astronomical, and to test all of them becomes completely infeasible.
So are there other approaches that can be used? It turns out that as illustrated in the picture below rule 30 has a property somewhat like the additive cellular automaton discussed two pages ago: in addition to allowing one row to be deduced from the row above, it allows columns to be deduced from columns to their right. But unlike for the additive cellular automaton, it takes not just one column but instead two adjacent columns to make this possible.
So if the encrypting sequence corresponds to a single column, how can one find an adjacent column? The last row of pictures below show a way to do this. One picks some sequence of cells for the right half of the top row, then evolves down the page. And somewhat surprisingly, it turns out that given the cells in one column, there are fairly few possibilities for what the neighboring column can be. So by sampling a limited number of sequences on the top row, one can often find a second column that then allows columns to the left to be determined, and thus for a candidate key to be found.

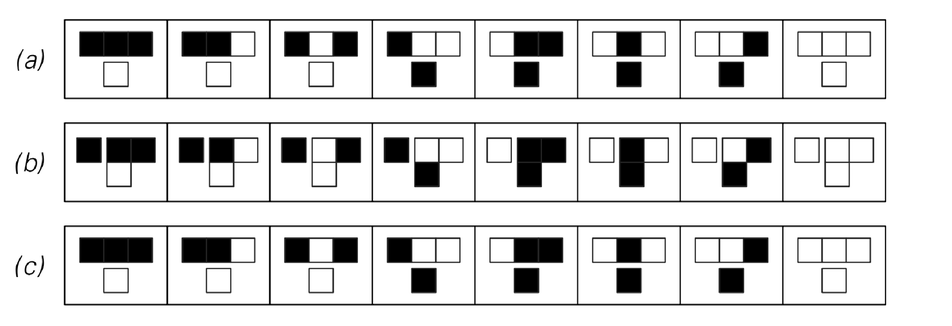
Sideways evolution in rule 30. (a) shows ordinary evolution from one row to the next. (b) shows evolution to the left starting from a pair of adjacent columns. (c) shows how a second column can be filled in from a row of cells to the right. The possibility of (b) is a consequence of one-sided additivity in rule 30; it leads to some level of cryptanalysis if the encrypting sequence consists of a complete column of cells.



