But it is rather easy to foil this particular approach to cryptanalysis: all one need do is not sample every single cell in a given column in forming the encrypting sequence. For without every cell there does not appear to be enough information for any kind of local rule to be able to deduce one column from others.

The picture below shows evidence for this. The cells marked by dots have colors that are taken as given, and then the colors of other cells are filled in according to the average that is obtained by starting from all possible initial conditions.

With two complete columns given, all cells to the left are determined to be either black or white. And with one complete column given, significant patches of cells still have determined colors. But if only every other cell in a column is given, almost nothing definite follows about the colors of other cells.

So what about the approach on page 602? Could this not be used here? It turns out that the approach relies crucially on the additivity of the underlying rules. And since rule 30 is not additive, it simply does not work. What happens is that the function that determines the color of a particular cell from the colors of cells in a nearby column rapidly becomes extremely

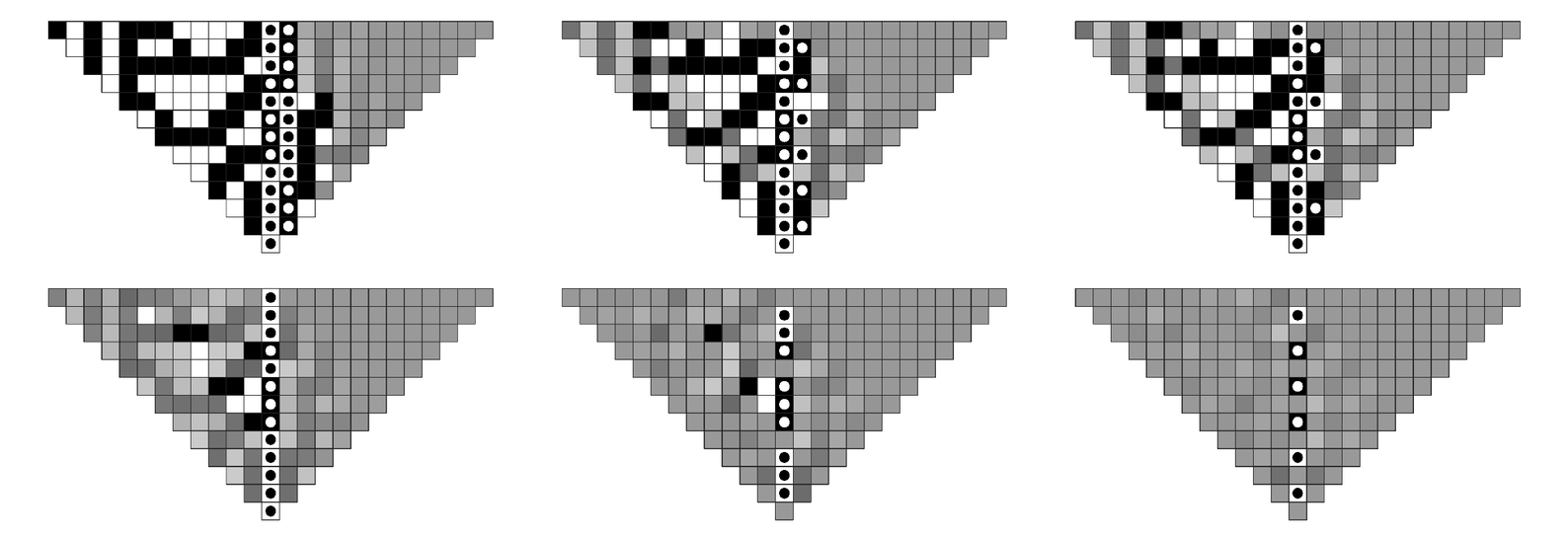
Patterns generated by rule 30 after averaging over all possible initial conditions that reproduce the arrangements of colors in the cells indicated by dots. If a cell is completely black or completely white then this means that its color is uniquely determined by the constraints given. If the cell is shown as gray then this means that it has some probability of being black and some probability of being white. Note that when two complete adjacent columns are specified all the cells on the left-hand side are determined. But when fewer cells are specified, the number of cells that are determined decreases rapidly, indicating that cryptanalysis is likely to become difficult.