So what happens if one considers more steps? As the pictures on the next page demonstrate, rules like 254 and 90 that have fairly simple behavior lead to formulas that stay fairly simple. But for rule 30 the formulas rapidly get much more complicated.

So this strongly suggests that no simple formula exists—at least of the type used here—that can describe patterns generated by any significant number of steps of evolution in a system like rule 30.

But what about formulas of other types? The formulas we have used so far can be thought of as always consisting of sums of products of variables. But what if we allow formulas with more general structure, not just two fixed levels of operations?

It turns out that any rule for blocks of black and white cells can be represented as some combination of just a single type of operation—for example a so-called Nand function of the kind often used in digital electronics. And given this, one can imagine finding for any particular rule the formula that involves the smallest number of Nand functions.

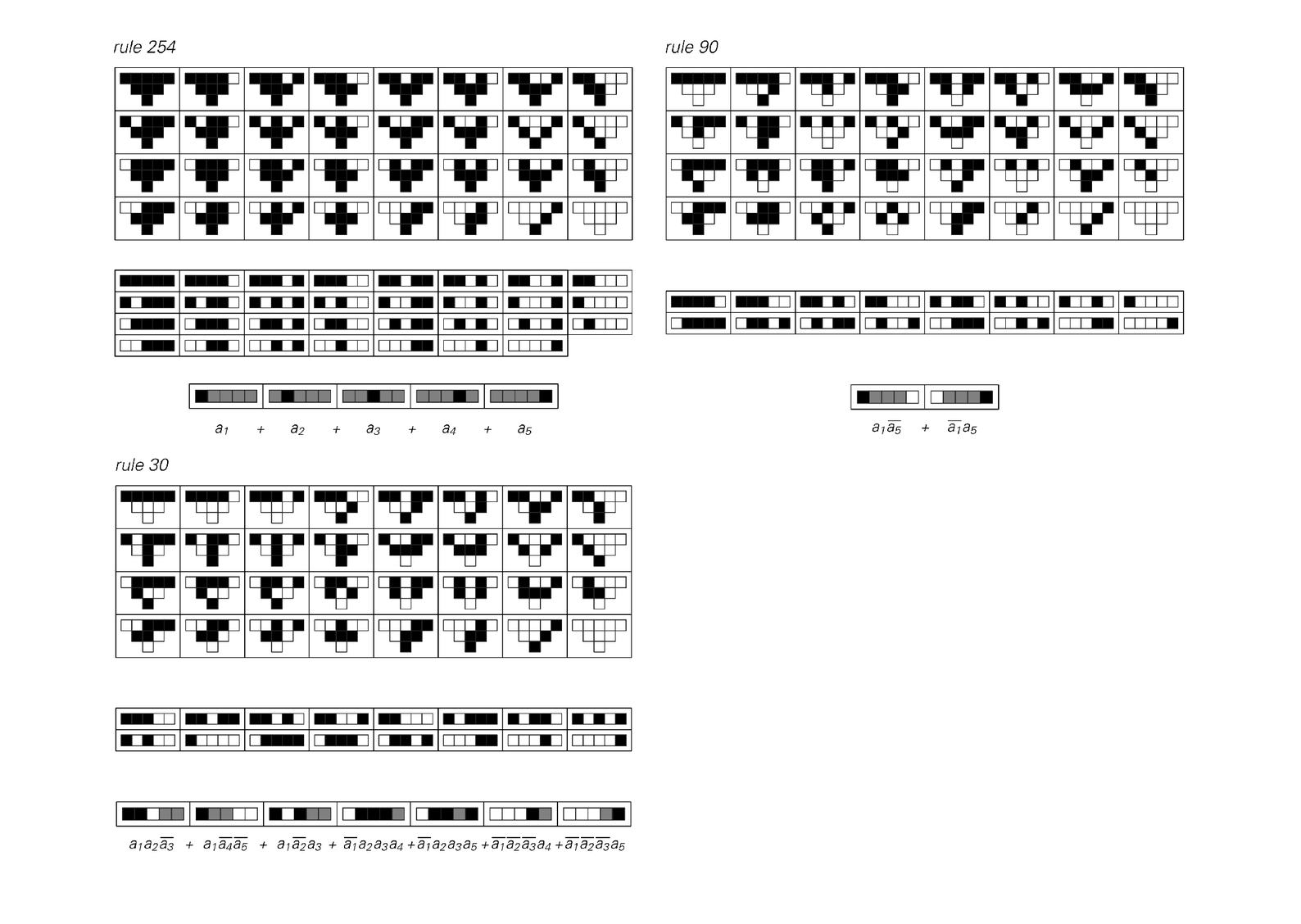
Boolean expression representations of the results from two steps in the evolution of three elementary cellular automata. At the top in each case is shown the explicit array of outcomes for each of the 32 possible initial configurations of cells. In the middle are shown those configurations that yield black cells. And at the bottom are the minimal representations of these collections of possibilities.