such simple formula. But even though no simple formula may exist, it is still always in principle possible to represent the outcome of any process of cellular automaton evolution by at least some kind of formula.
The picture below shows how this can be done for a single step in the evolution of three elementary cellular automata. The basic idea is to translate the rule for a given cellular automaton into a formula that depends on three variables a1, a2 and a3 whose values correspond to the colors of the three initial cells. The formula consists of a sum of terms, with each term being zero unless the colors of the three cells match a situation in which the rule yields a black cell.
In the first instance, each term can be set up to correspond directly to one of the cases in the original rule. But in general this will lead to a more complicated formula than is necessary. For as the picture demonstrates, it is often possible to combine several cases into one term by ignoring the values of some of the variables.
The picture at the top of the facing page shows what happens if one considers two steps of cellular automaton evolution. There are now altogether five variables, but at least for rules like rules 254 and 90 the individual terms end up not depending on most of these variables.
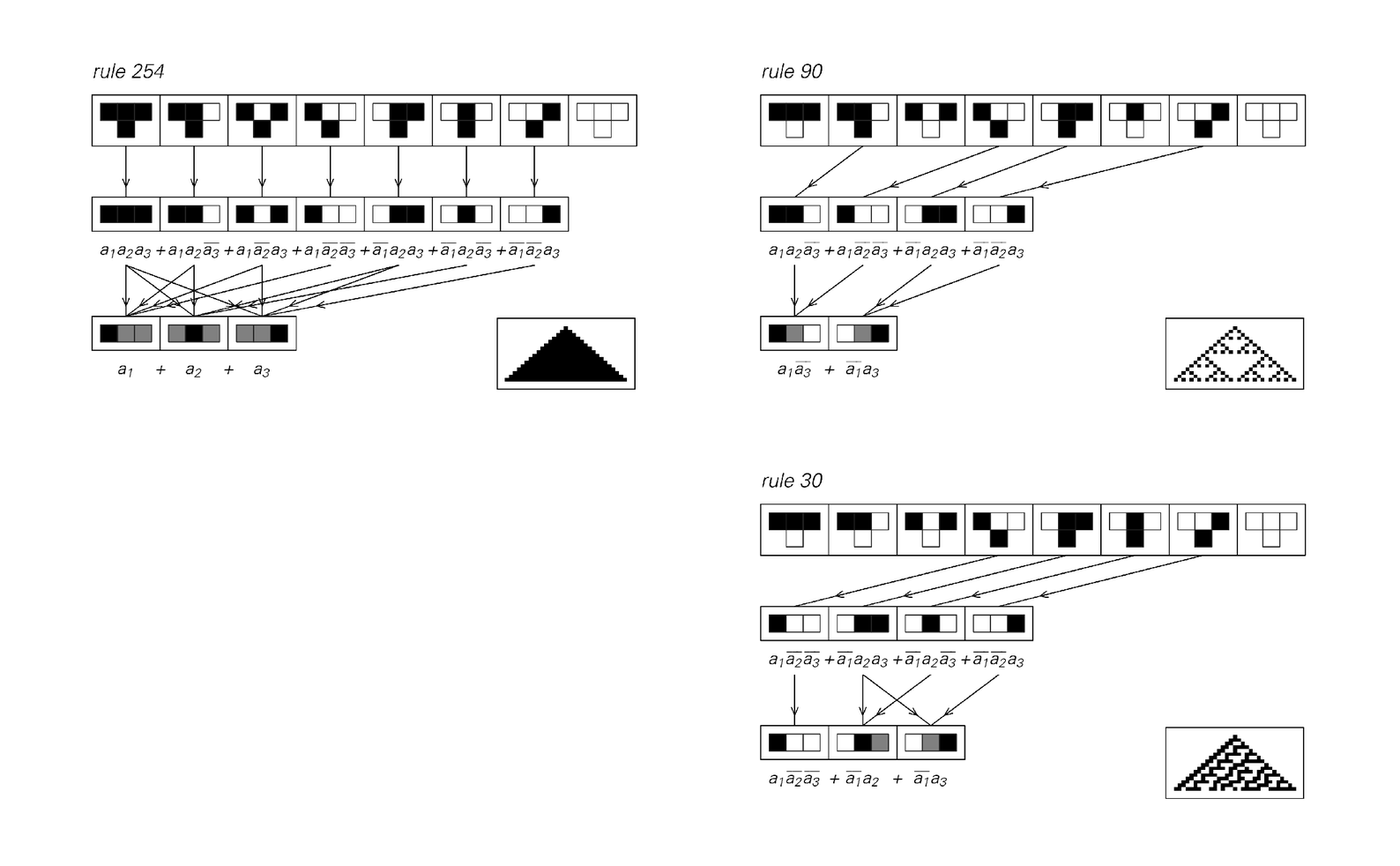
Boolean expression representations of the rules for three elementary cellular automata. The first row shows the original cellular automaton rules. The second row shows those combinations of cells that yield a black cell according to each of the rules. The third row shows a minimized version in which gray cells are introduced to indicate either black or white. In the formulas under the second and third rows the variable ai represents the color of the ith cell. ei ej is analogous to ei ∧ ej, ei + ej to ei ∨ ej, and 