As the pictures at the top of the facing page demonstrate, the overall patterns produced in all cases tend to look complex, and in many respects random. But the crucial point is that because of the way the system was constructed there is nevertheless a simple formula for the color of each cell: it is given just by a particular digit in the number obtained by raising the multiplier to a power equal to the number of steps. So despite their apparent complexity, all the patterns on the facing page can in effect be described by simple traditional mathematical formulas.
But if one thinks about actually using such formulas one might at first wonder what good they really are. For if one was to work out the value of a power mt by explicitly performing t multiplications, this would be very similar to explicitly following t steps of cellular automaton evolution. But the point is that because of certain mathematical features of powers it turns out to be possible—as indicated in the table below—to find mt with many fewer than t operations; indeed, one or two operations for every base 2 digit in t is always for example sufficient.
So what about other patterns produced by cellular automata and similar systems? Is it possible that in the end all such patterns could just be described by simple mathematical formulas? I do not think so. In fact, as I will argue in Chapter 12, my strong belief is that in the vast majority of cases it will be impossible for quite fundamental reasons to find any
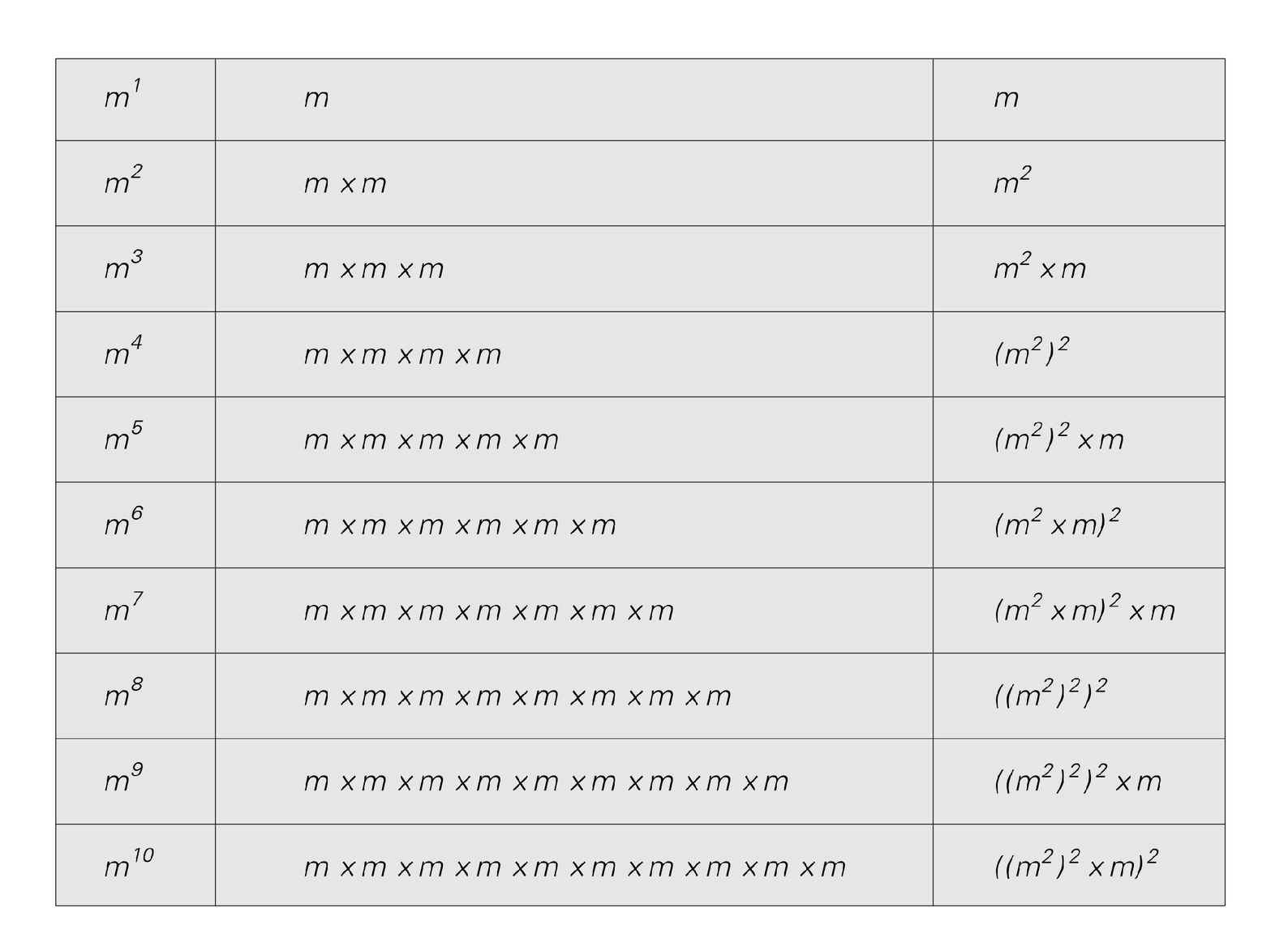
Examples of how powers can be computed more efficiently than by successive multiplications. In the cases shown, the choice of whether to square or multiply by an additional factor of m at each step in computing mt is made on the basis of the successive digits in the base 2 representation of the number t.