automaton all cells are always effectively treated as being exactly the same. And to emulate a mobile automaton with a cellular automaton it turns out that all one need do is to divide the possible colors of cells in the cellular automaton into two sets: lighter ones that correspond to ordinary cells in the mobile automaton, and darker ones that correspond to active cells. And then by setting up appropriate rules and choosing initial conditions that contain only one darker cell, one can produce in the cellular automaton an exact emulation of every step in the evolution of a mobile automaton—as in the picture below.
The same basic approach can be used to construct a cellular automaton that emulates a Turing machine, as illustrated on the next page. Once again, lighter colors in the cellular automaton represent ordinary cells in the Turing machine, while darker colors represent the cell under the head, with a specific darker color corresponding to each possible state of the head.
One might think that the reason that mobile automata and Turing machines can be emulated by cellular automata is that they both consist of fixed arrays of cells, just like cellular automata. So then one may wonder what happens with substitution systems, for example, where there is no fixed array of elements.
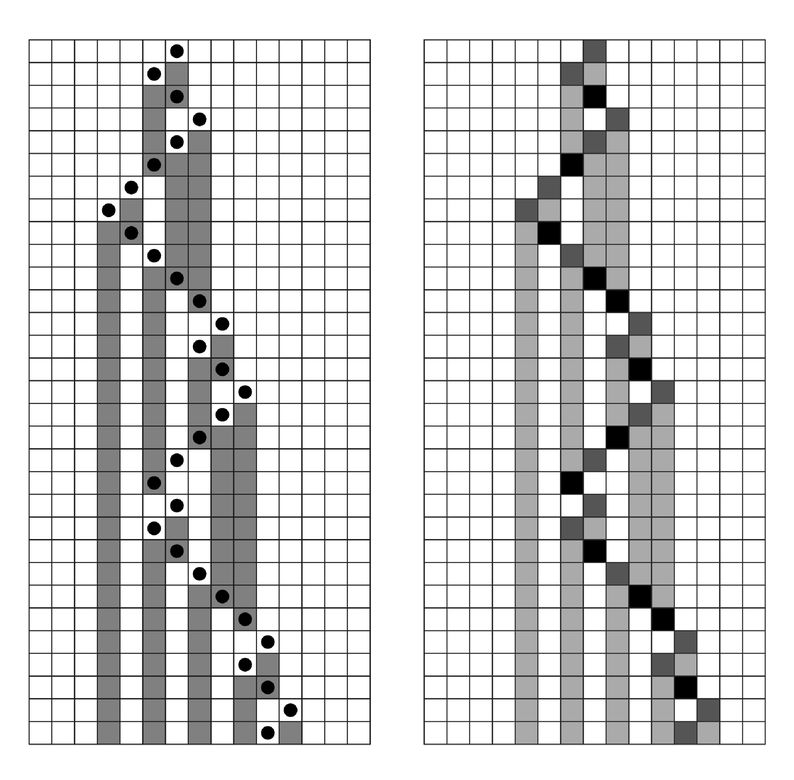 |  |
An example of a mobile automaton (see page 71) being emulated by a cellular automaton. In the mobile automaton shown on the left each cell has two possible colors. In the cellular automaton shown on the right, the cells have four possible colors, with two darker colors corresponding to the active cell in the mobile automaton. The rules for the mobile automaton and the cellular automaton are shown above. In the rules for the cellular automaton, ![]() indicates a cell of any color.
indicates a cell of any color.



