The pictures on the facing page demonstrate that in fact these can also be emulated by cellular automata. But while one can emulate each step in the evolution of a mobile automaton or a Turing machine with a single step of cellular automaton evolution, this is no longer in general true for substitution systems.
That this must ultimately be the case one can see from the fact that the total number of elements in a substitution system can be multiplied by a factor from one step to the next, while in a cellular automaton the size of a pattern can only ever increase by a fixed amount at each step. And what this means is that it can take progressively larger numbers of cellular automaton steps to reproduce each successive step in the evolution of the substitution system—as illustrated in the pictures on the facing page.
The same kind of problem occurs in sequential substitution systems—as well as in tag systems. But once again, as the pictures on page 660 demonstrate, it is still perfectly possible to emulate systems like these using cellular automata.
But just how broad is the set of systems that cellular automata can ultimately emulate? All the examples of systems that I have shown so far can at some level be thought of as involving sequences of elements that are fairly directly analogous to the cells in a cellular automaton.
 | 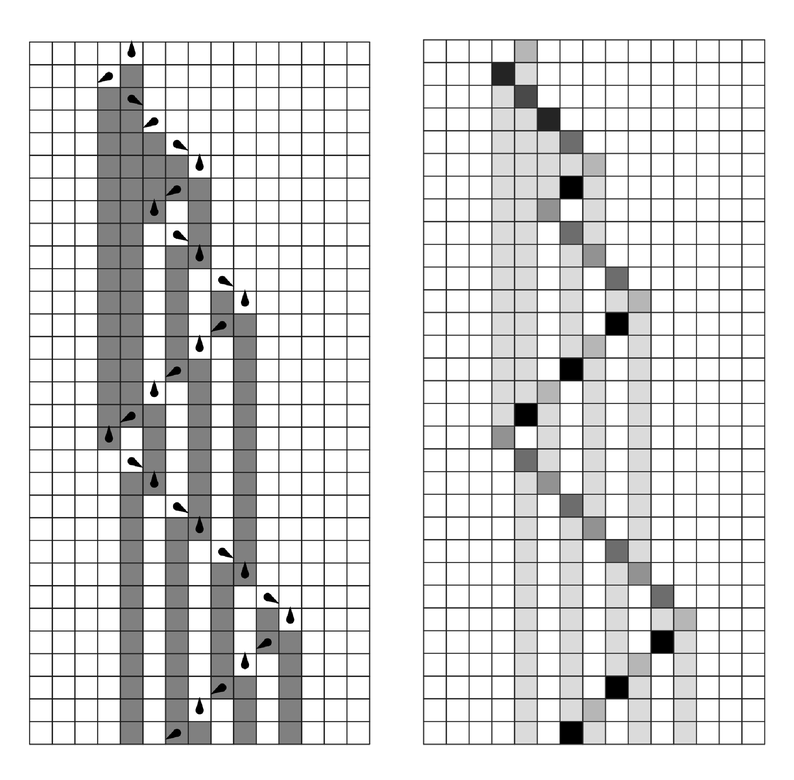 |
An example of a Turing machine being emulated by a cellular automaton. In the Turing machine on the left each cell has two possible colors, and the head has three possible states. In the cellular automaton, the cells have eight possible colors, with the lightest two colors being used for cells not at the position of the head. The rules for the Turing machine and the cellular automaton are shown above. In the rules for the cellular automaton, ![]() indicates a cell of any color.
indicates a cell of any color.



