Universality in Turing Machines and Other Systems
From the results of the previous few sections [8, 9, 10, 11], we now have some idea where the threshold for universality lies in cellular automata. But what about other kinds of systems—like Turing machines? How complicated do the rules need to be in order to get universality?
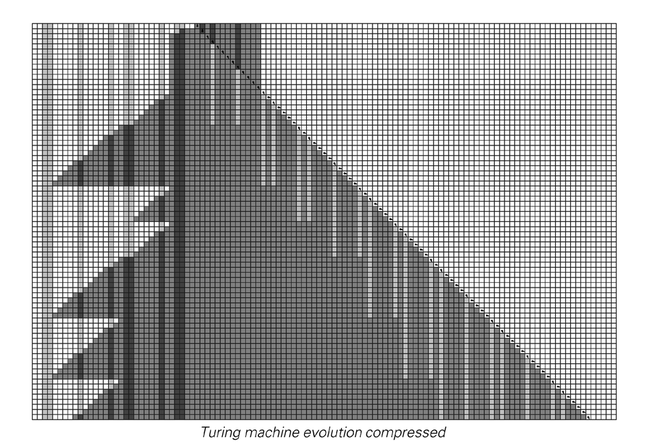
In the 1950s and early 1960s a certain amount of work was done on trying to construct small Turing machines that would be universal. The main achievement of this work was the construction of the universal machine with 7 states and 4 possible colors shown below.
The rule for a universal Turing machine with 7 states and 4 colors constructed in 1962. Until now, this was essentially the simplest known universal Turing machine. Note that one element of the rule can be considered as specifying that the Turing machine should "halt" with the head staying in the same location and same state.
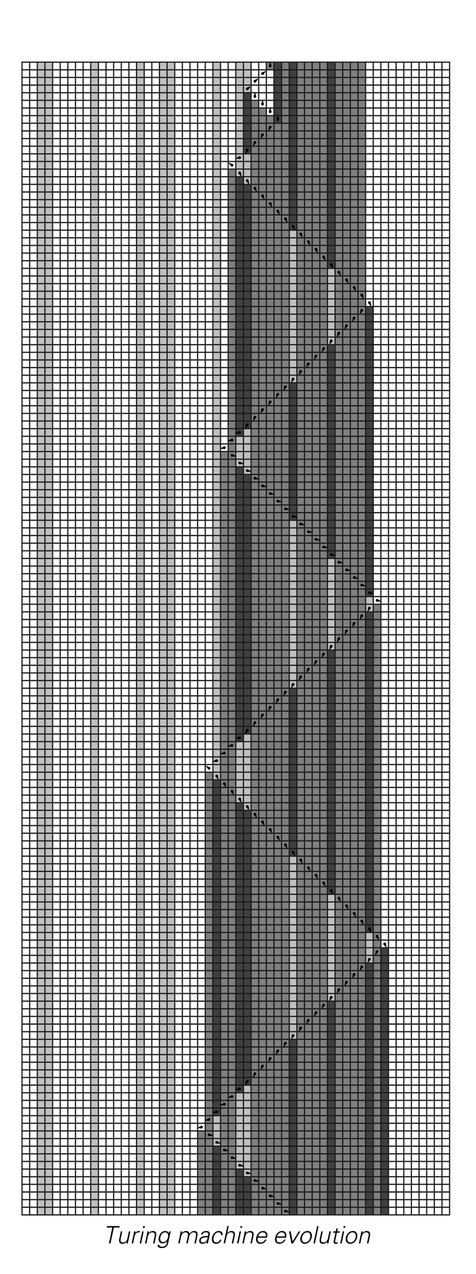 | 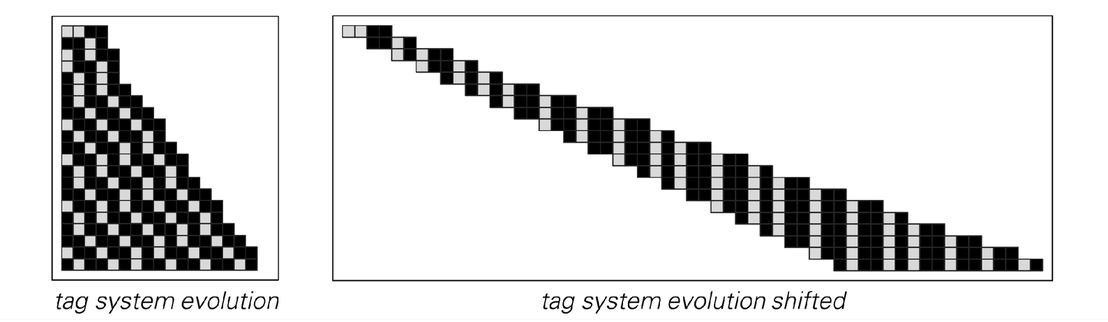   |
An example of how the Turing machine above can emulate a tag system. A black element in the tag system is set up to correspond to a block of four cells in the Turing machine, while a white element corresponds to a single cell.