But can this detailed kind of phenomenon really be used as the basis for doing fundamentally more sophisticated computations? To compare the general computational capabilities of continuous and discrete systems one needs to find some basic scheme for constructing inputs and decoding outputs that one can use in both types of systems. And the most obvious and practical approach is to require that this always be done by finite discrete processes.
But at least in this case it seems fairly clear that none of the simple functions shown below can for example ever lead to results that go beyond ones that could readily be generated by the evolution of ordinary discrete systems. And the same is presumably true if one works with essentially any of what are normally considered standard mathematical functions. But what happens if one assumes that one can set up a system that not only finds values of such functions but also finds solutions to arbitrary equations involving them?
With pure polynomial equations one can deduce from results in algebra that no fundamentally more sophisticated computations become possible. But as soon as one even allows trigonometric functions, for example, it turns out that it becomes possible to construct equations for which finding a solution is equivalent to finding
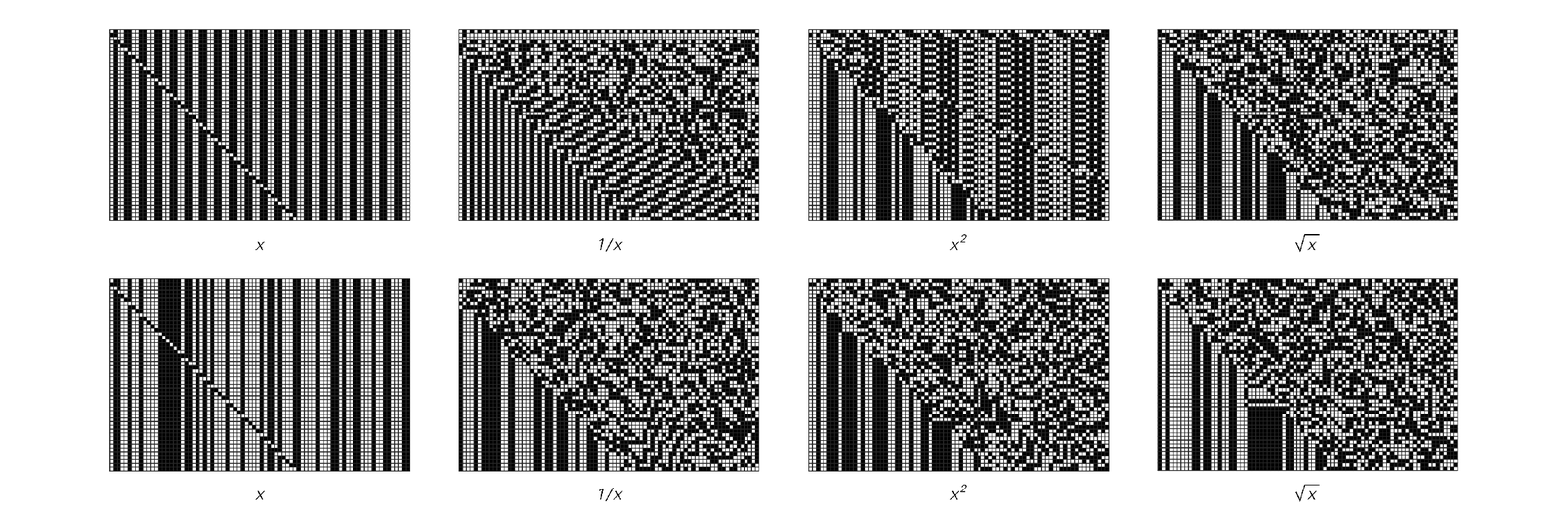
Results from mathematical operations on numbers with similar digit sequences. Each successive line in each picture gives the digit sequence obtained by using a value of x in which one successive digit has been reversed. The top row of pictures start from the repetitive base 2 digit sequence of x=3/5; the bottom row of pictures from x=π/4. The lack of coherence between successive digit sequences in each picture reflects the non-locality of mathematical operations when applied to digit sequences.



