and 2 colors. And as the pictures on the facing page show, different Turing machines can take very different numbers of steps to do the computations they do.
Turing machine (a), for example, always finishes its computation after at most 5 steps, independent of the length of its input. But in most of the other Turing machines shown, the maximum number of steps needed generally increases with the length of the input.
Turing machines (b), (c) and (d) are ones that always compute the same function. But while this means that for a given input each of them yields the same output, the pictures demonstrate that they usually take a different number of steps to do so. Nevertheless, if one looks at the maximum number of steps needed for any given length of input one finds that this still always increases exactly linearly—just as for the Turing machines that add 1 shown at the top of this page.
So are there cases in which there is more rapid growth? Turing machine (e) shows an example in which the maximum number of steps grows like the square of the length of the input. And it turns out that at least among 2-state 2-color Turing machines this is the only one that computes the function it computes—so that at least if one wants to use a program this simple there is no faster way to do the computation.
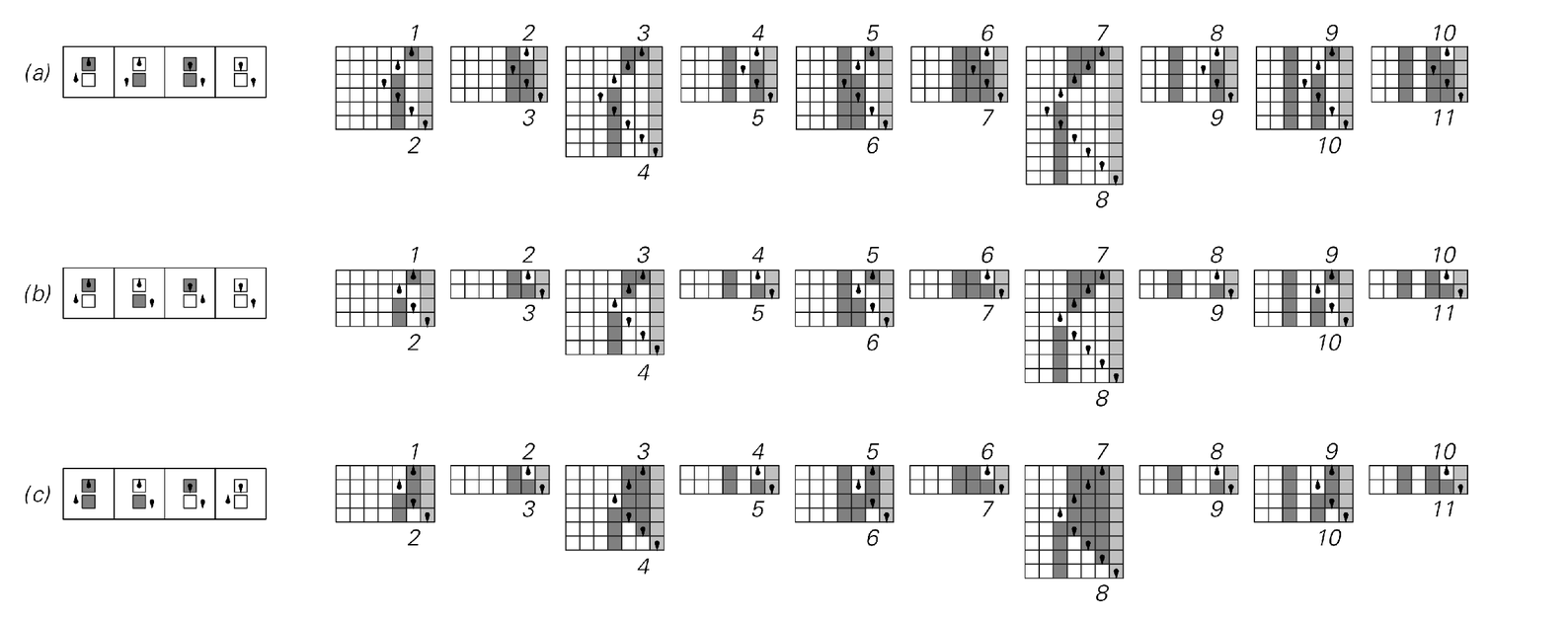
The three schemes for adding 1 to a number that are used by Turing machines with 2 states and 2 colors. All show the same linear growth in maximum number of steps as their size of input increases. This growth can be viewed as a consequence of potentially having to propagate carry digits from one end of the input number to the other. The machines shown are numbered 445, 461 and 1512.