
 | 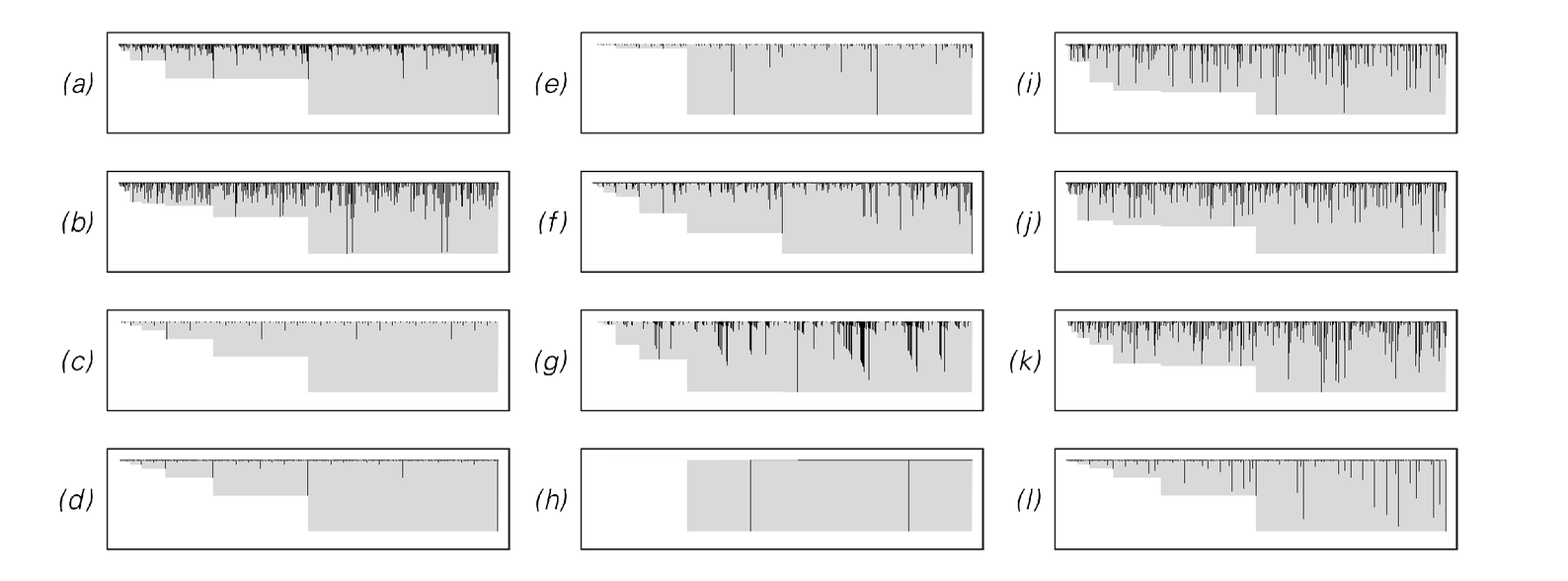 |
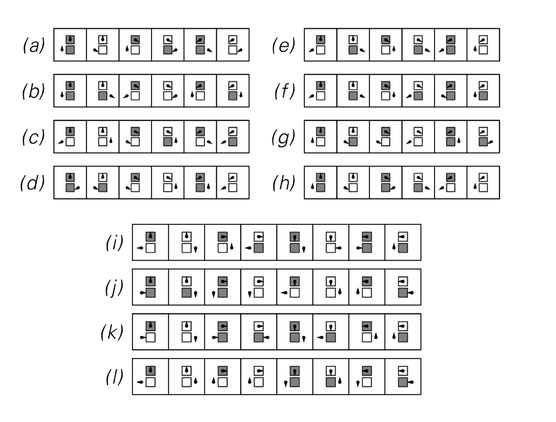
Examples of Turing machines with 3 and 4 states in which the maximum number of steps before a computation is finished grows at least exponentially with the length of the input. In all cases no Turing machines with the same number of states compute the same functions in fewer steps. In case (h) the number of steps grows so rapidly that only two peaks are seen in the plot. The top row of pictures are all scaled to be exactly the same height, even though the initial conditions cannot be chosen to make the number of steps in each case anything more than roughly the same. The machines have numbers: 582285, 657939, 2018806, 2868668, 2138664, 2139050, 132527, 600720, 3374234978, 1806221583, 1232059922, 3238044559. Cases like (c) and (d) show nested behavior reminiscent of a counter which generates digit sequences of successive integers.



