Indeed, my expectation is that asking about possible outcomes of t steps of evolution will already be NP-complete even for the rule 30 cellular automaton, as illustrated below.
Just as with the Turing machines of pages 761 and 763 there will be a certain density of cases where the problem is fairly easy to solve. But it seems likely that as one increases t, no ordinary Turing machine or cellular automaton will ever be able to guarantee to solve the problem in a number of steps that grows only like some power of t.
Yet even so, there could still in principle exist in nature some other kind of system that would be able to do this. And for example one might imagine that this would be possible if one were able to use exponentially small components. But almost all the evidence we have
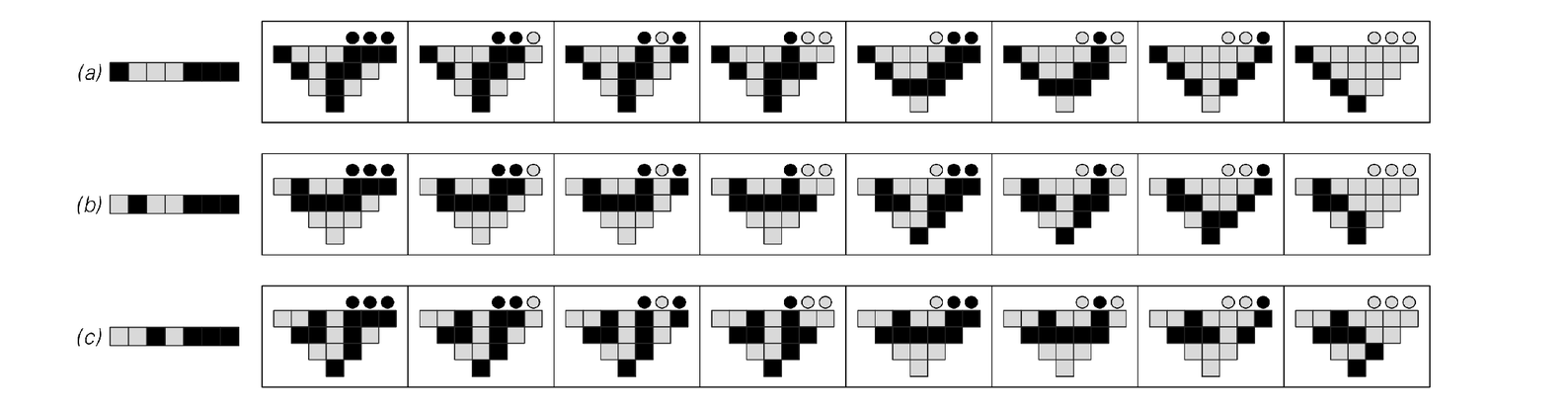

Example of a simple problem that I suspect is NP-complete. The problem is to determine whether right-hand cells in the initial conditions for rule 30 can be filled in so as to produce a vertical black stripe of a certain height at the bottom of the center column formed after t steps of evolution. The pictures at the top show that in case (a) stripes up to height 3 can be produced, in case (b) up to height 2, and in case (c) only up to height 1. The pictures at the bottom indicate in black for which of the 2t + 1 successive left-hand sequences of t + 1 cells it is impossible to get stripes of respectively heights 1 and 2. The apparent randomness of these patterns reflects the likely difficulty of the problem. The problem is related to issues of rule 30 cryptanalysis discussed on page 603.



