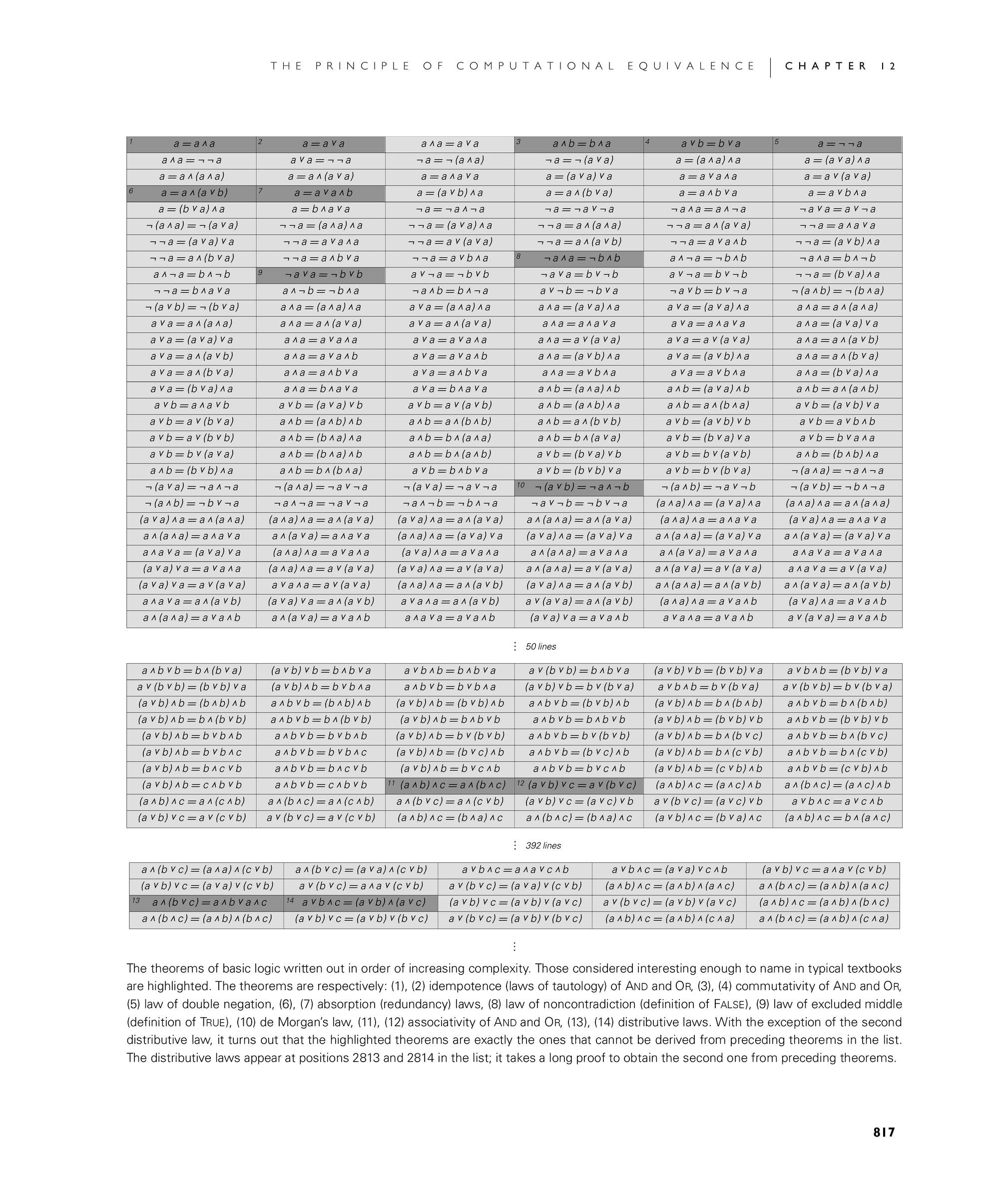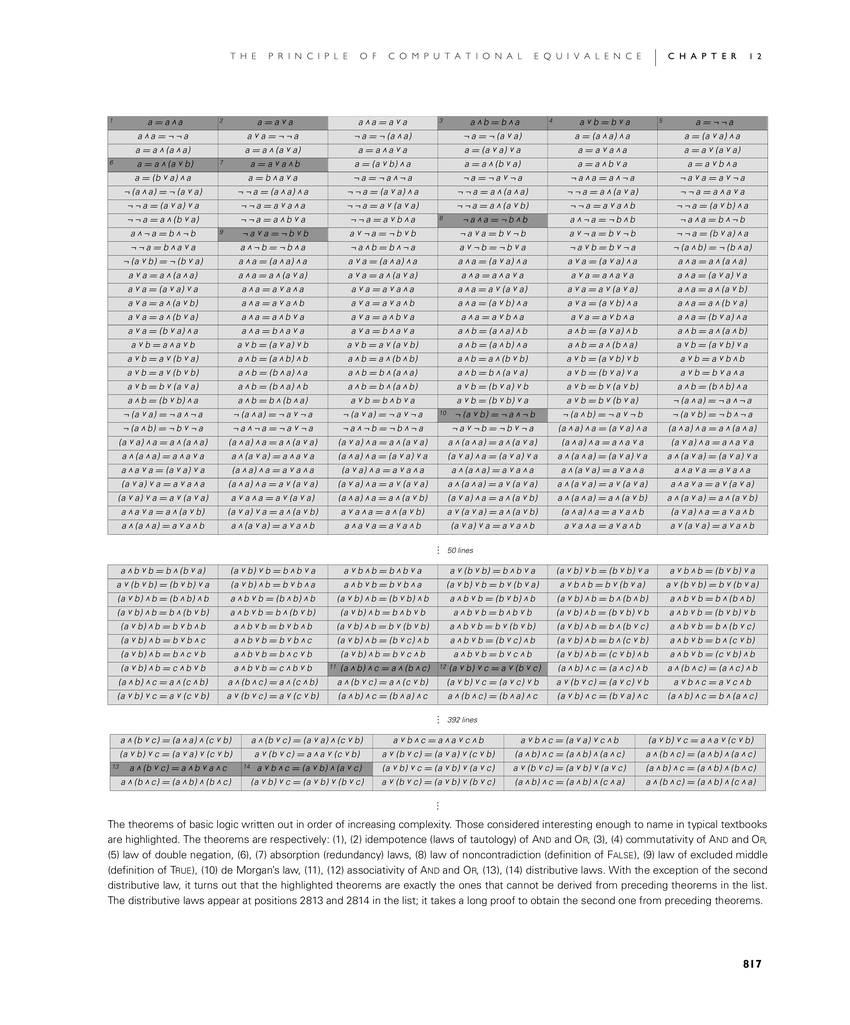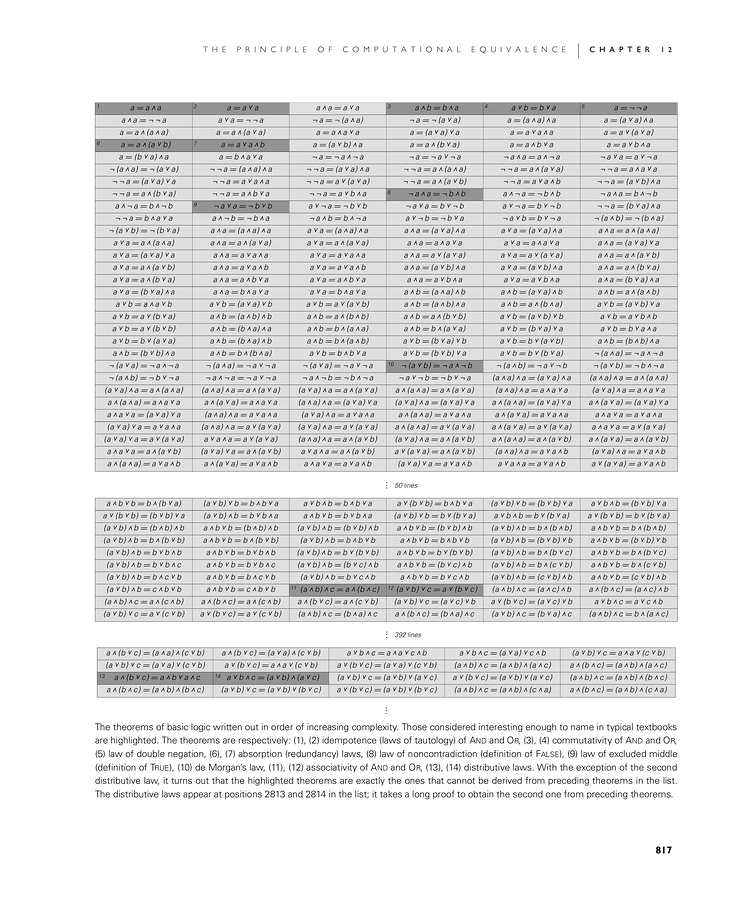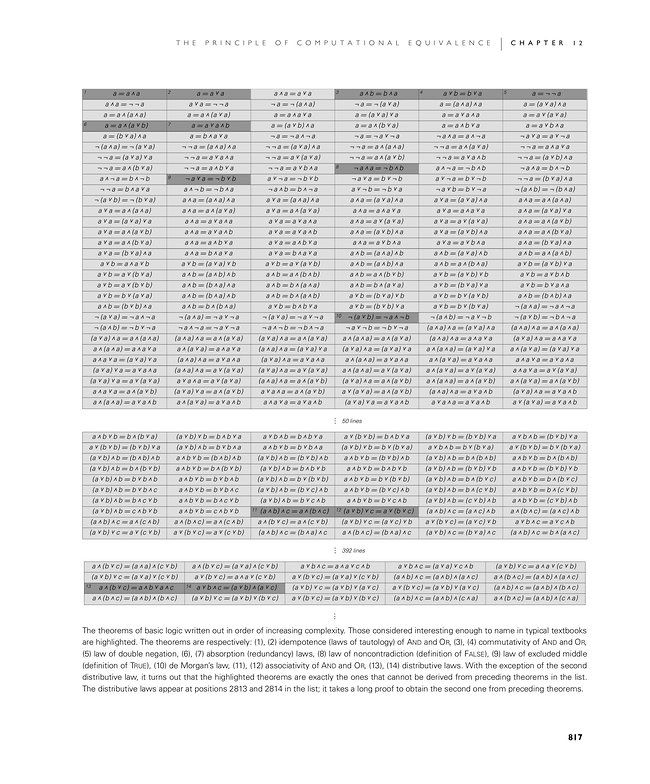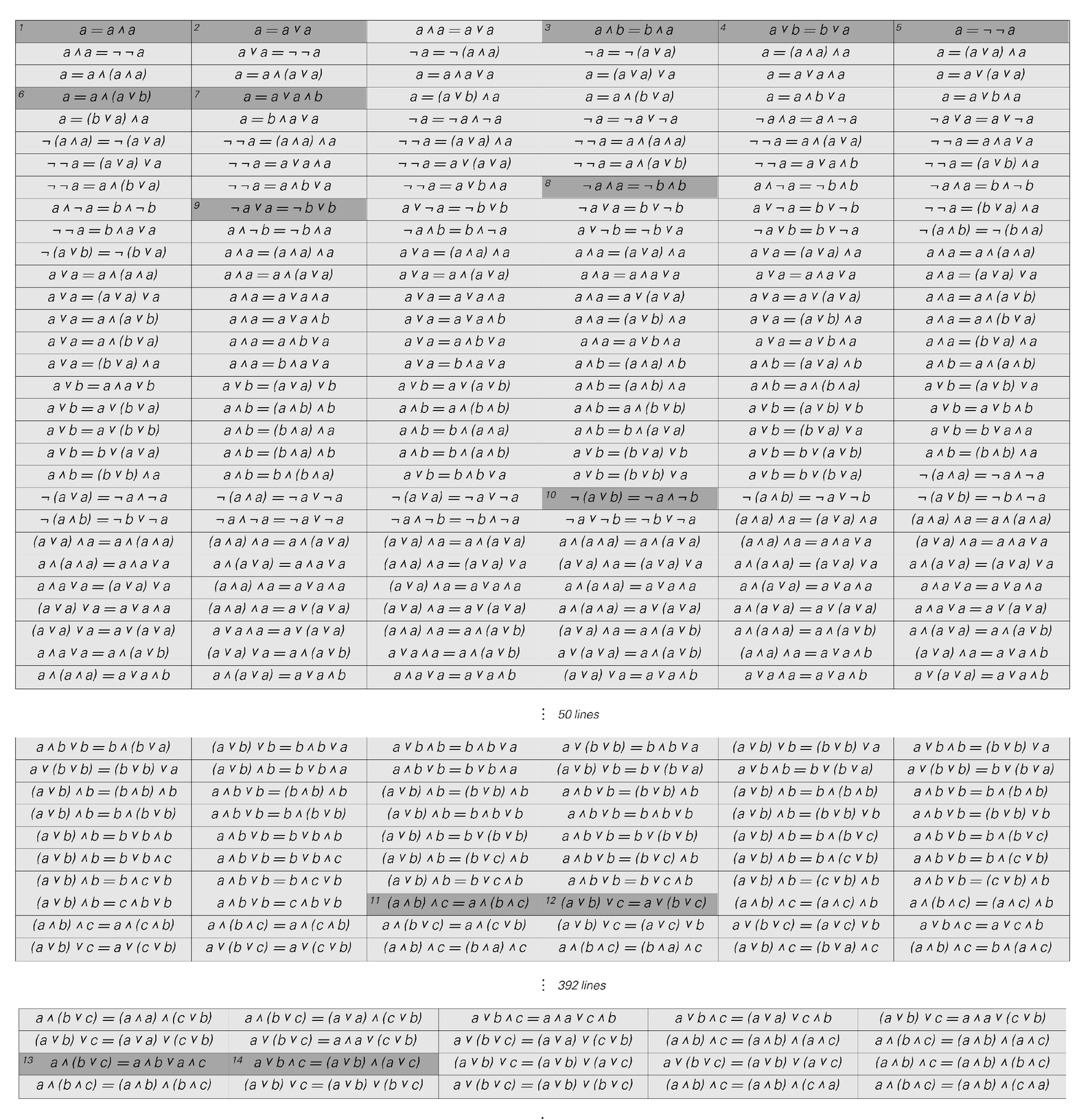
The theorems of basic logic written out in order of increasing complexity. Those considered interesting enough to name in typical textbooks are highlighted. The theorems are respectively: (1), (2) idempotence (laws of tautology) of And and Or, (3), (4) commutativity of And and Or, (5) law of double negation, (6), (7) absorption (redundancy) laws, (8) law of noncontradiction (definition of False), (9) law of excluded middle (definition of True), (10) de Morgan's law, (11), (12) associativity of And and Or, (13), (14) distributive laws. With the exception of the second distributive law, it turns out that the highlighted theorems are exactly the ones that cannot be derived from preceding theorems in the list. The distributive laws appear at positions 2813 and 2814 in the list; it takes a long proof to obtain the second one from preceding theorems.