But what determines which theorems these will be? One might have thought that it would be purely a matter of history. But actually looking at the list of theorems it always seems that the interesting ones are in a sense those that show the least unnecessary complication.
And indeed if one starts from the beginning of the list one finds that most of the theorems can readily be derived from simpler ones earlier in the list. But there are a few that cannot—and that therefore provide in a sense the simplest statements of genuinely new information. And remarkably enough what I have found is that these theorems are almost exactly the ones highlighted on the previous page that have traditionally been identified as interesting.
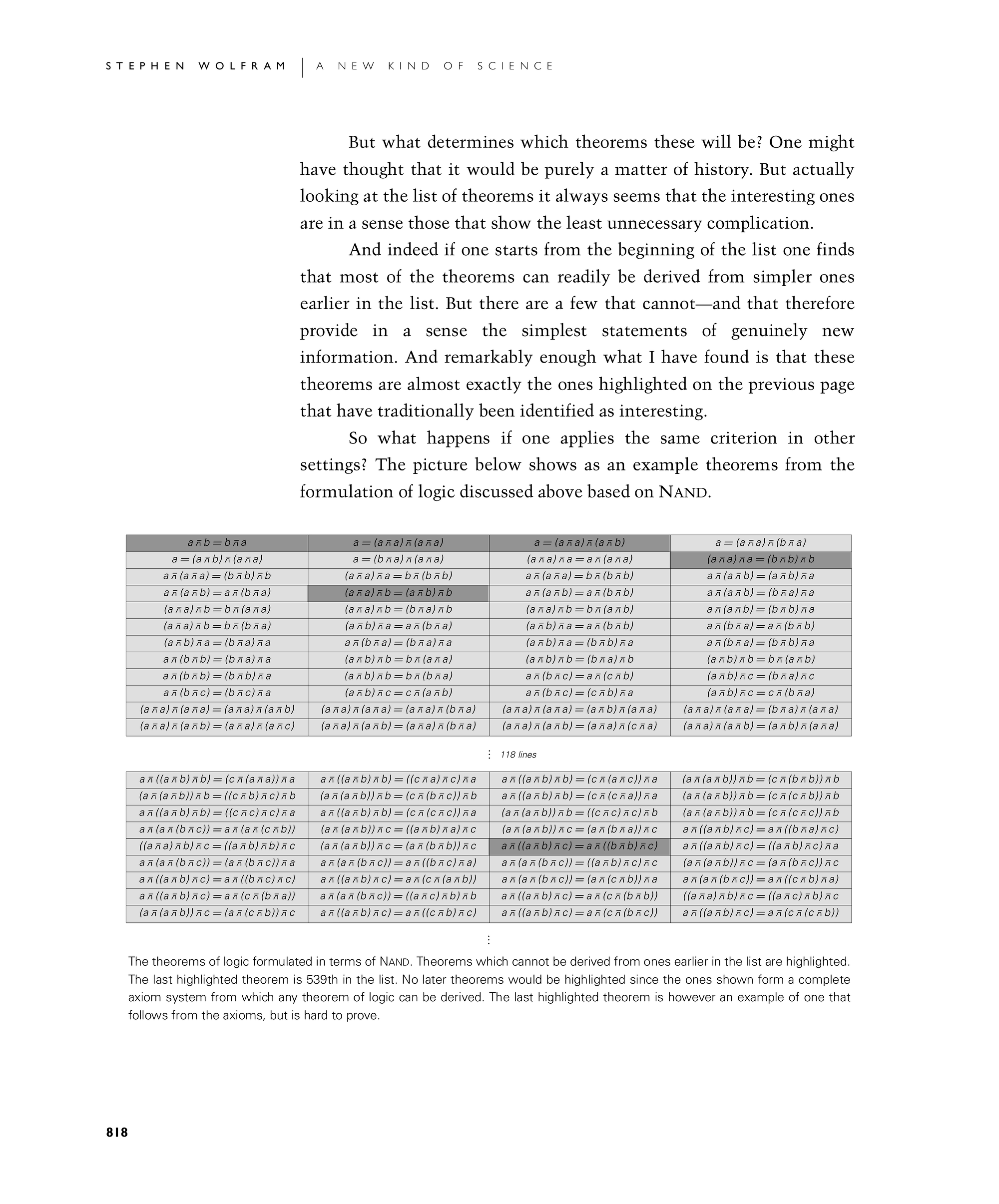
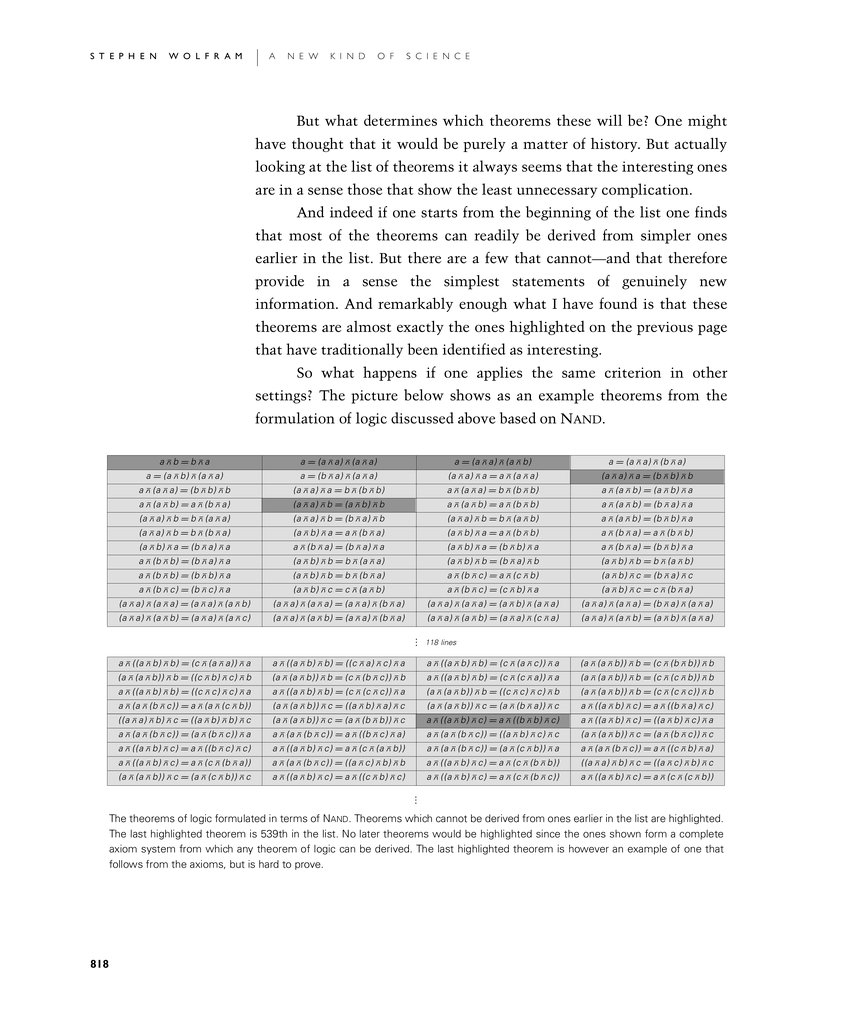
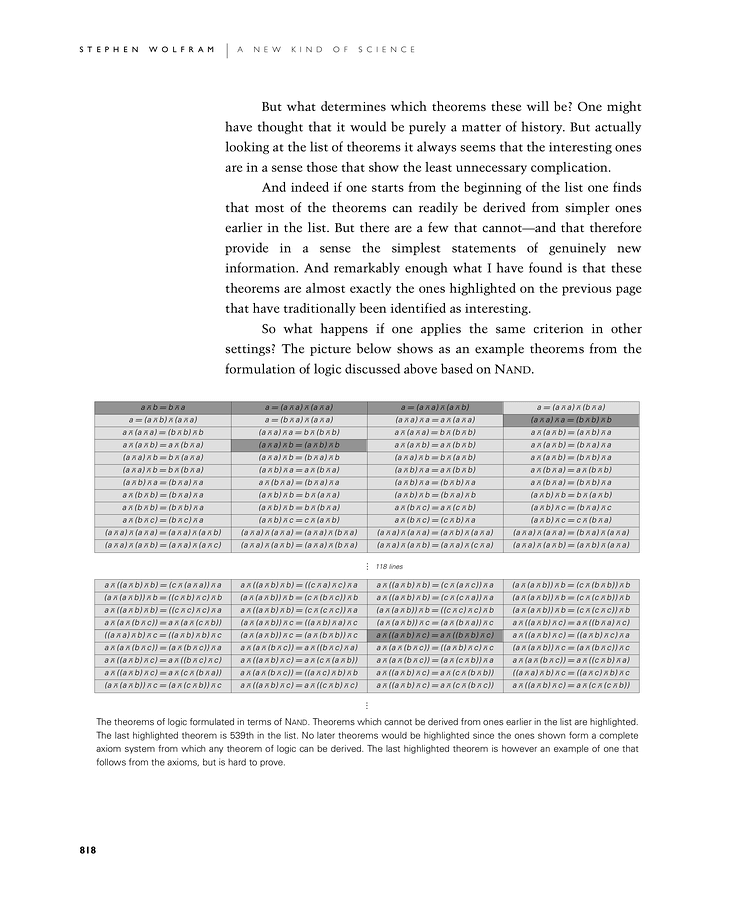
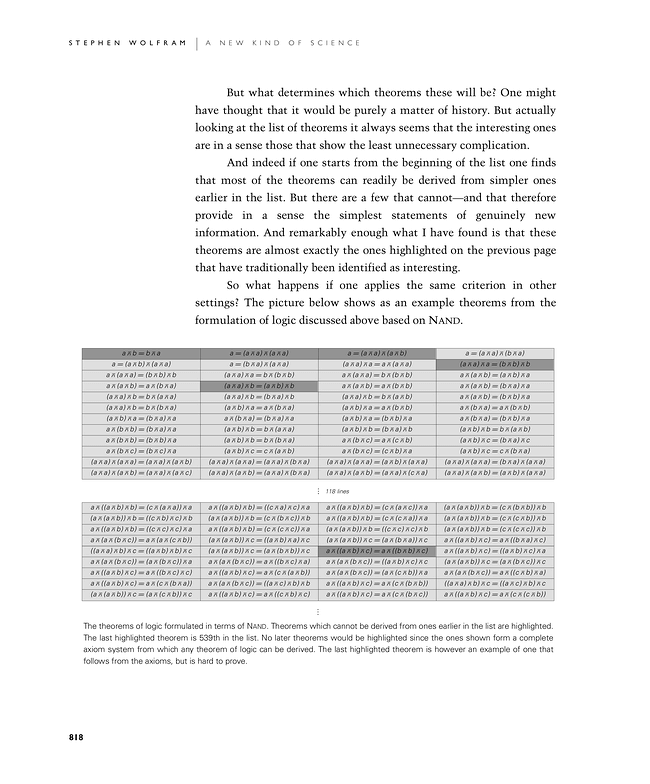
So what happens if one applies the same criterion in other settings? The picture below shows as an example theorems from the formulation of logic discussed above based on Nand.
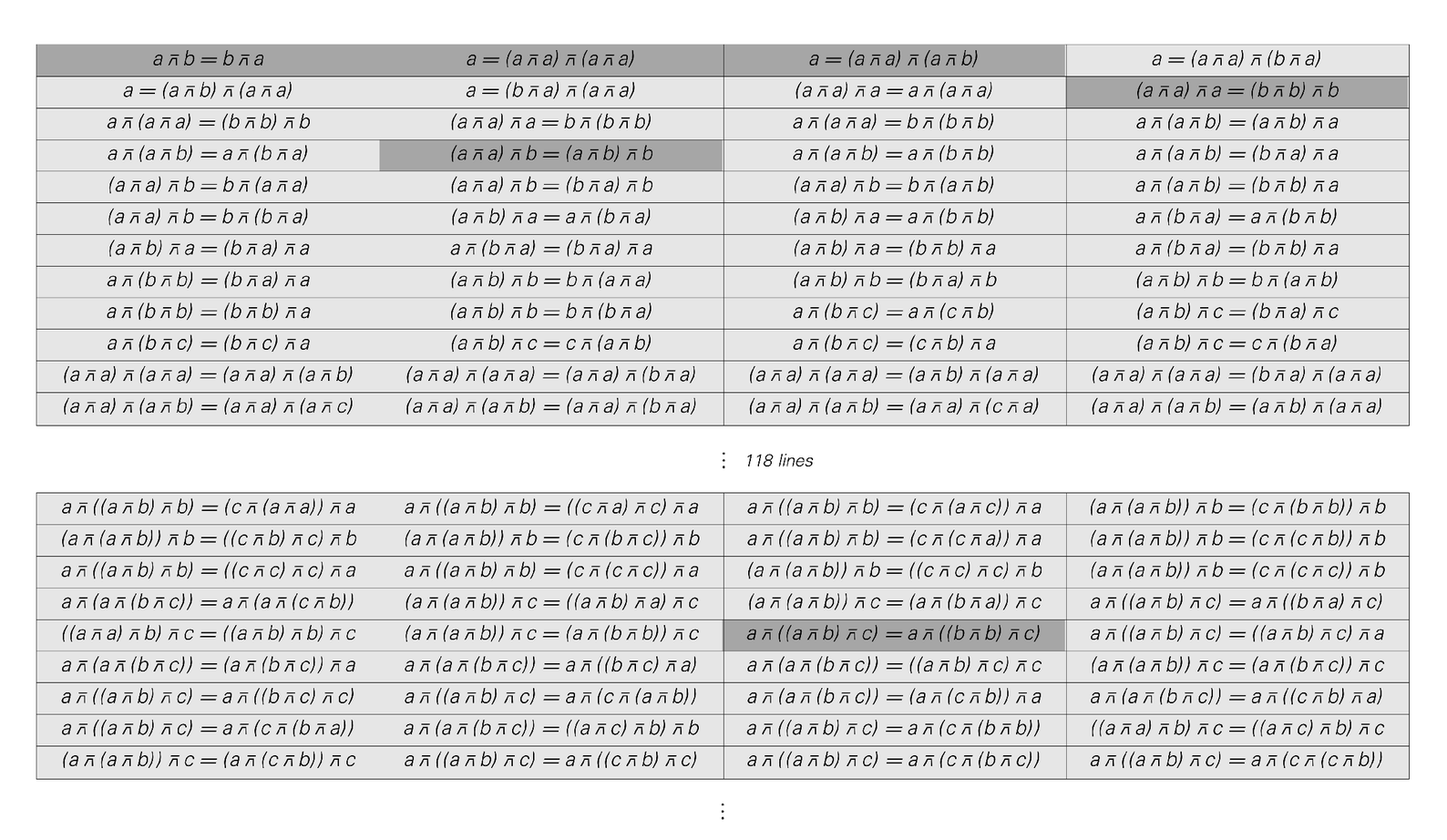
The theorems of logic formulated in terms of Nand. Theorems which cannot be derived from ones earlier in the list are highlighted. The last highlighted theorem is 539th in the list. No later theorems would be highlighted since the ones shown form a complete axiom system from which any theorem of logic can be derived. The last highlighted theorem is however an example of one that follows from the axioms, but is hard to prove.