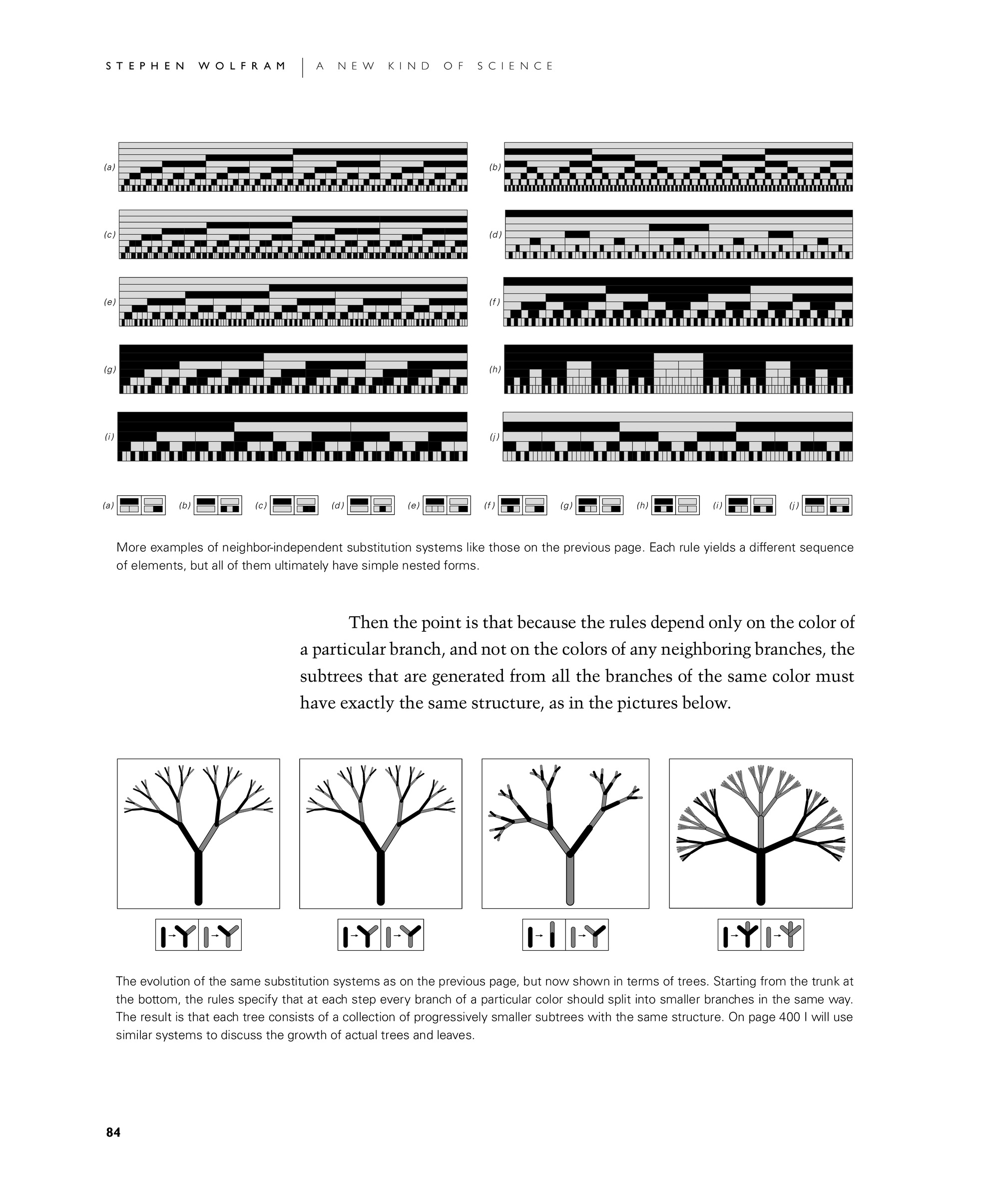
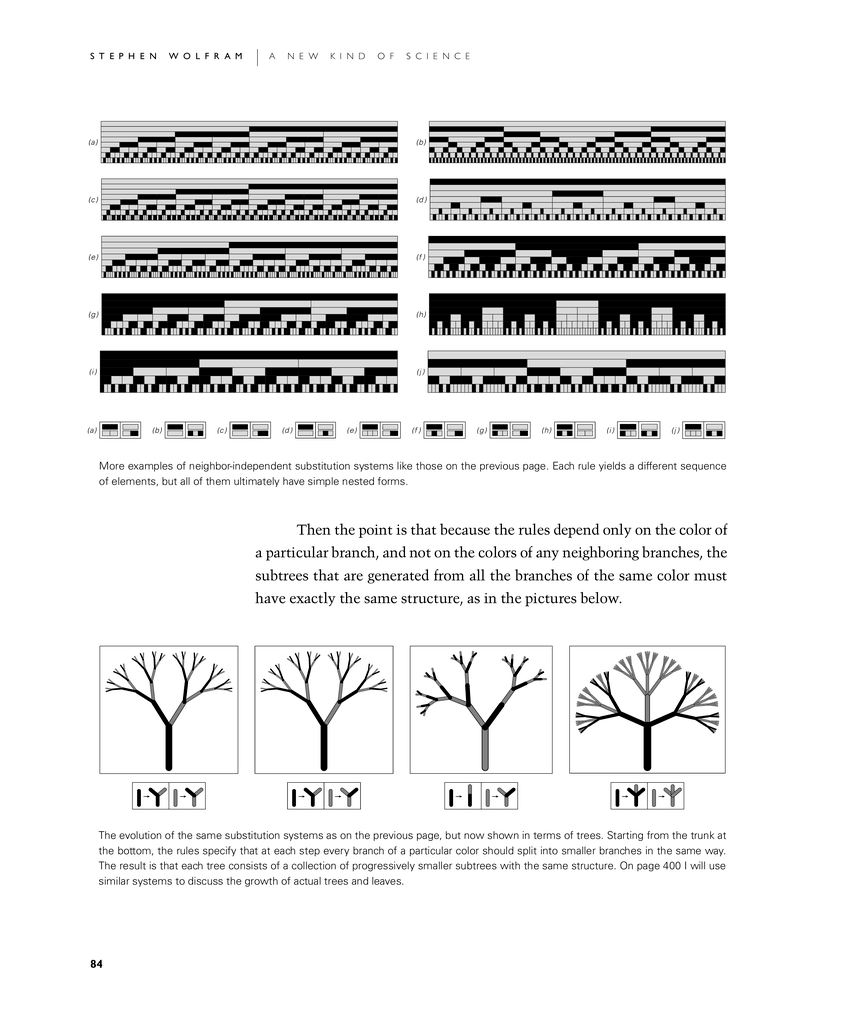
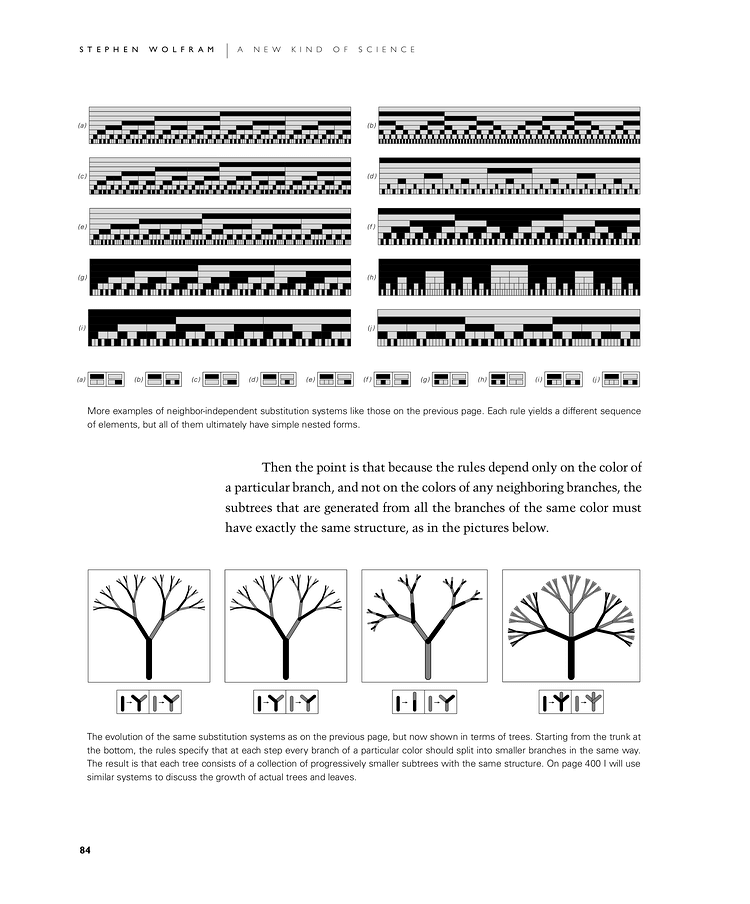
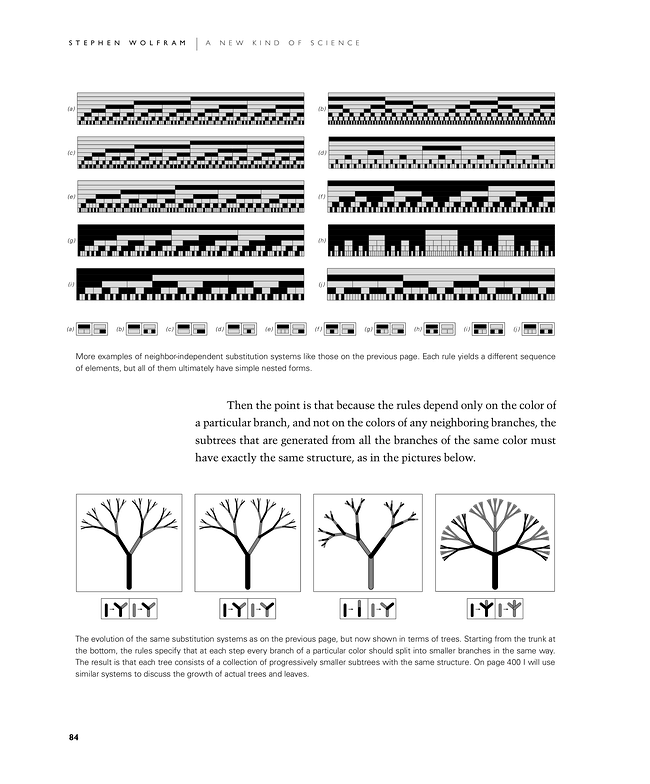
Then the point is that because the rules depend only on the color of a particular branch, and not on the colors of any neighboring branches, the subtrees that are generated from all the branches of the same color must have exactly the same structure, as in the pictures below.

More examples of neighbor-independent substitution systems like those on the previous page. Each rule yields a different sequence of elements, but all of them ultimately have simple nested forms.
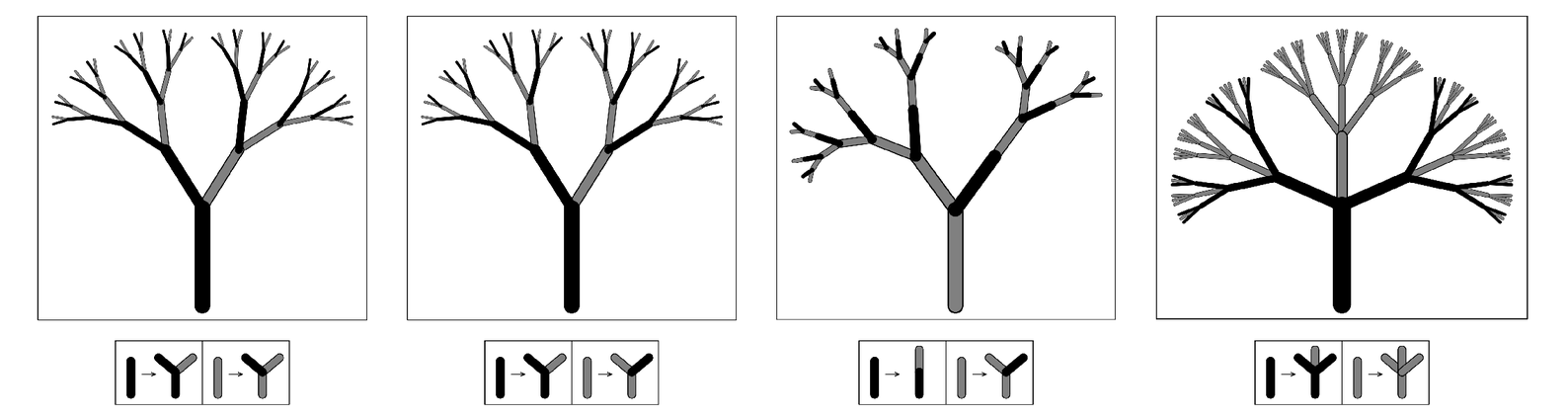
The evolution of the same substitution systems as on the previous page, but now shown in terms of trees. Starting from the trunk at the bottom, the rules specify that at each step every branch of a particular color should split into smaller branches in the same way. The result is that each tree consists of a collection of progressively smaller subtrees with the same structure. On page 400 I will use similar systems to discuss the growth of actual trees and leaves.