cellular automata with rules as simple as the ones we have been using these three forms of behavior would be all that we could ever get.
But the remarkable fact is that this turns out to be wrong.
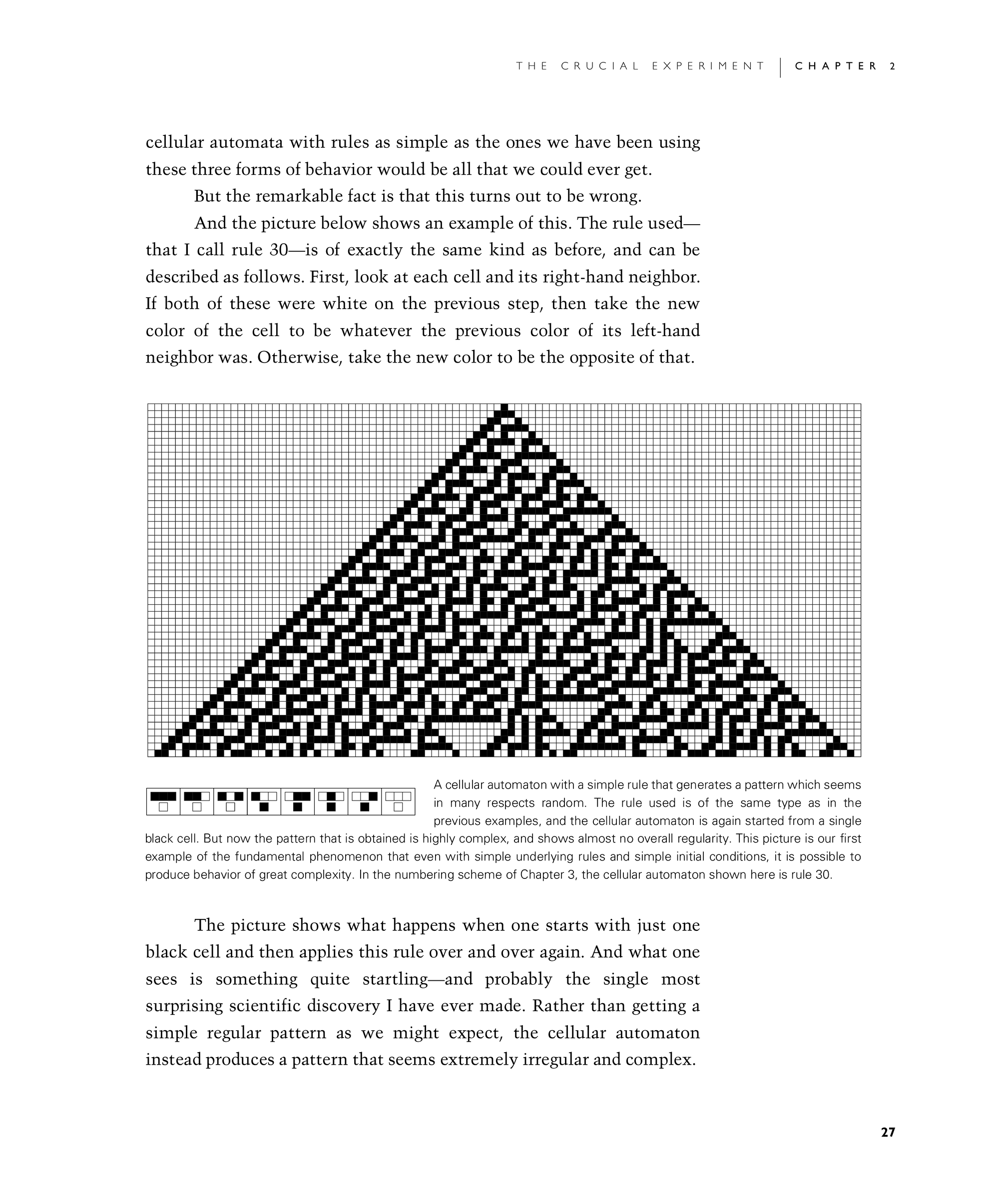
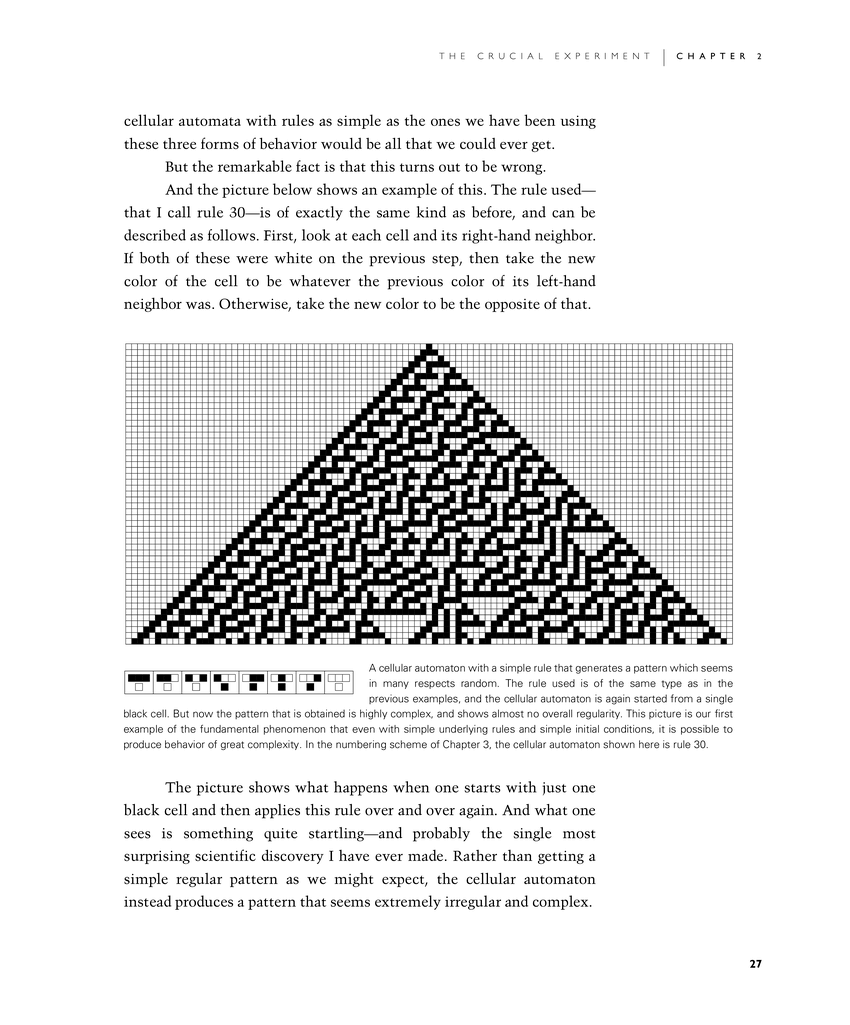
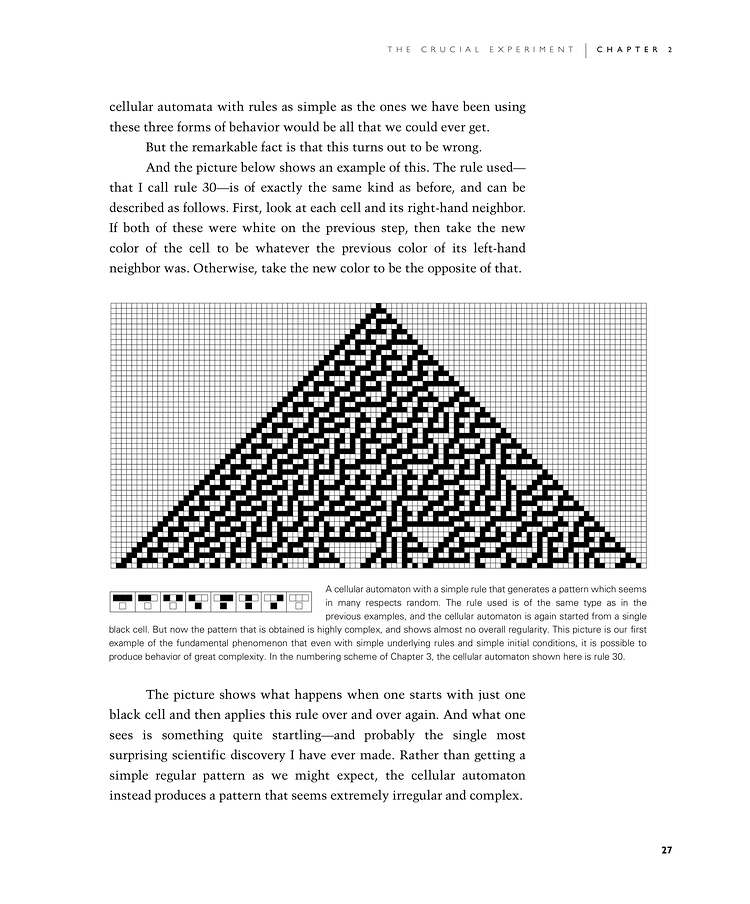
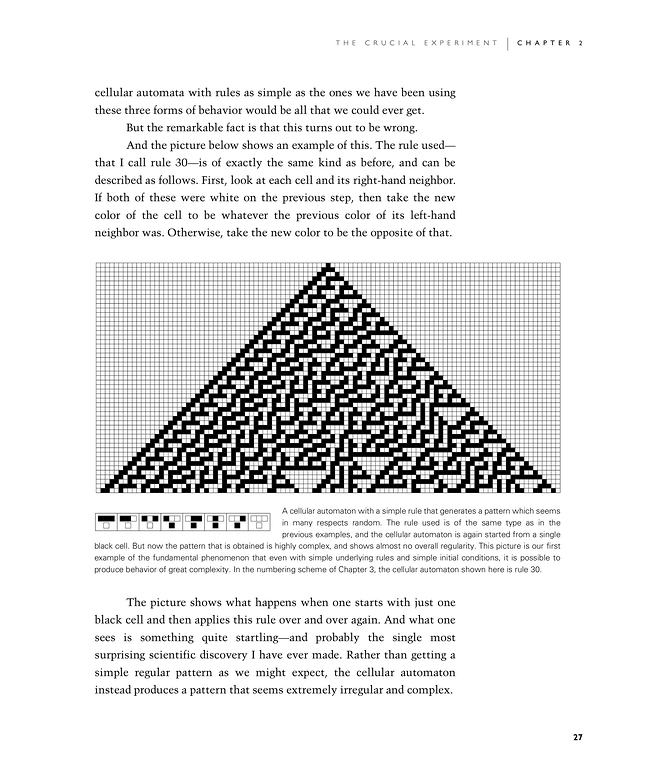
And the picture below shows an example of this. The rule used—that I call rule 30—is of exactly the same kind as before, and can be described as follows. First, look at each cell and its right-hand neighbor. If both of these were white on the previous step, then take the new color of the cell to be whatever the previous color of its left-hand neighbor was. Otherwise, take the new color to be the opposite of that.
The picture shows what happens when one starts with just one black cell and then applies this rule over and over again. And what one sees is something quite startling—and probably the single most surprising scientific discovery I have ever made. Rather than getting a simple regular pattern as we might expect, the cellular automaton instead produces a pattern that seems extremely irregular and complex.

A cellular automaton with a simple rule that generates a pattern which seems in many respects random. The rule used is of the same type as in the previous examples, and the cellular automaton is again started from a single black cell. But now the pattern that is obtained is highly complex, and shows almost no overall regularity. This picture is our first example of the fundamental phenomenon that even with simple underlying rules and simple initial conditions, it is possible to produce behavior of great complexity. In the numbering scheme of Chapter 3, the cellular automaton shown here is rule 30.