And as the bottom pictures on the previous page demonstrate, the forms of these patterns are very sensitive to the precise angle of successive elements: indeed, even a small deviation leads to patterns that are visually quite different. At first one might have assumed that to get a precise angle like 137.5° would require some kind of elaborate and highly detailed process. But just as in so many other situations that we have seen in this book, what we have seen is that in fact a very simple rule is all that is in the end needed.
One of the general features of plants is that most of their cells tend to develop fairly rigid cellulose walls which make it essentially impossible for new material to be added inside the volume of the plant, and so typically force new growth to occur only on the outside of the plant—most importantly at the tips of stems.
But when plants form sheets of material as in leaves or petals there is usually some flexibility for growth to occur within the sheet. And the pictures below show examples of what can happen if one starts with a flat disk and then adds different amounts of material in different places.
If more material is added near the center than near the edge, as in case (b), then the disk is forced to take on a cup shape similar to many
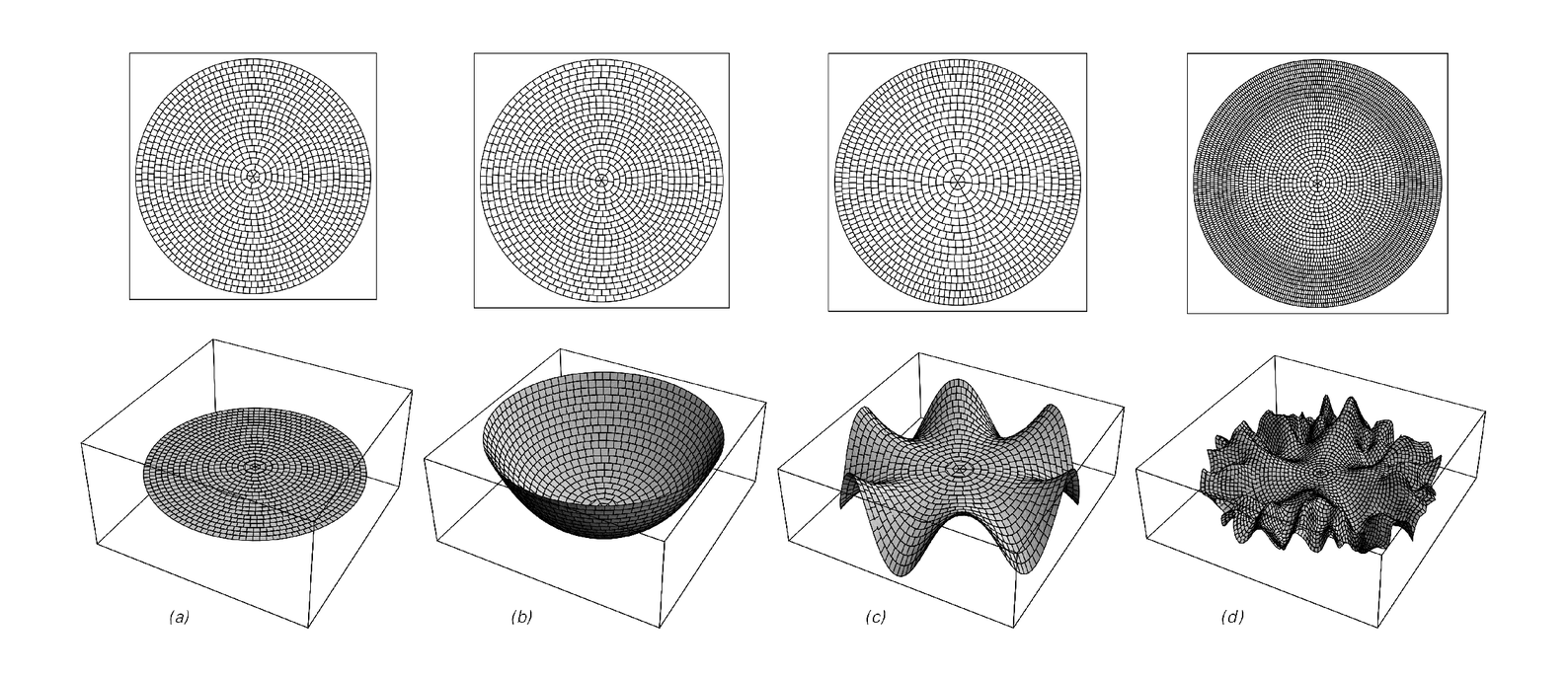
Disks with varying amounts of material at different distances from their centers. In the top row the disks are always flat, forcing the cells of material to vary in size and shape. In the bottom row, the disks form shapes in three dimensions in which all cells are the same size and shape. Relative to case (a), the amount of material going out from the center decreases linearly in case (b), increases linearly in case (c), and increases exponentially in case (d).



