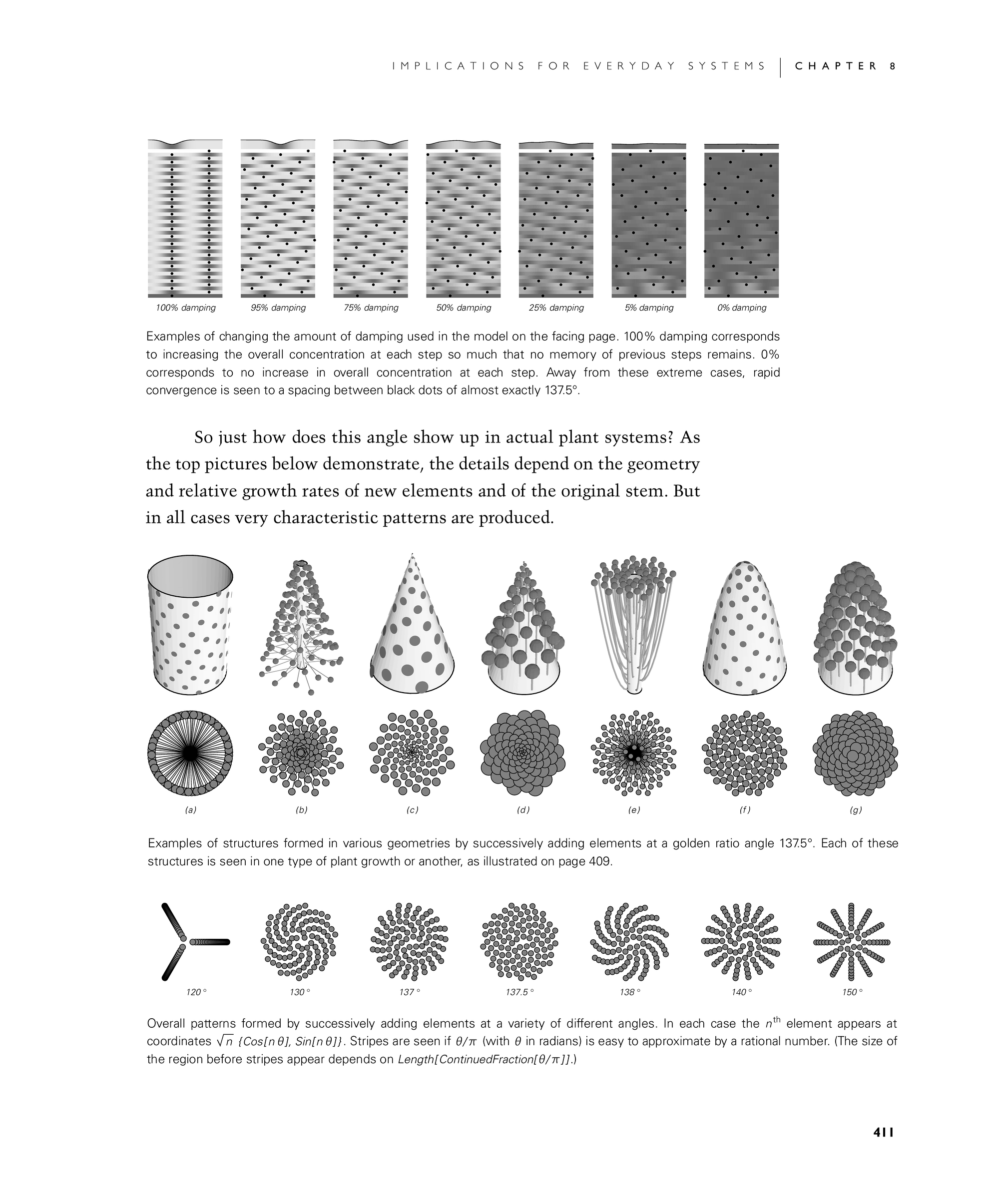
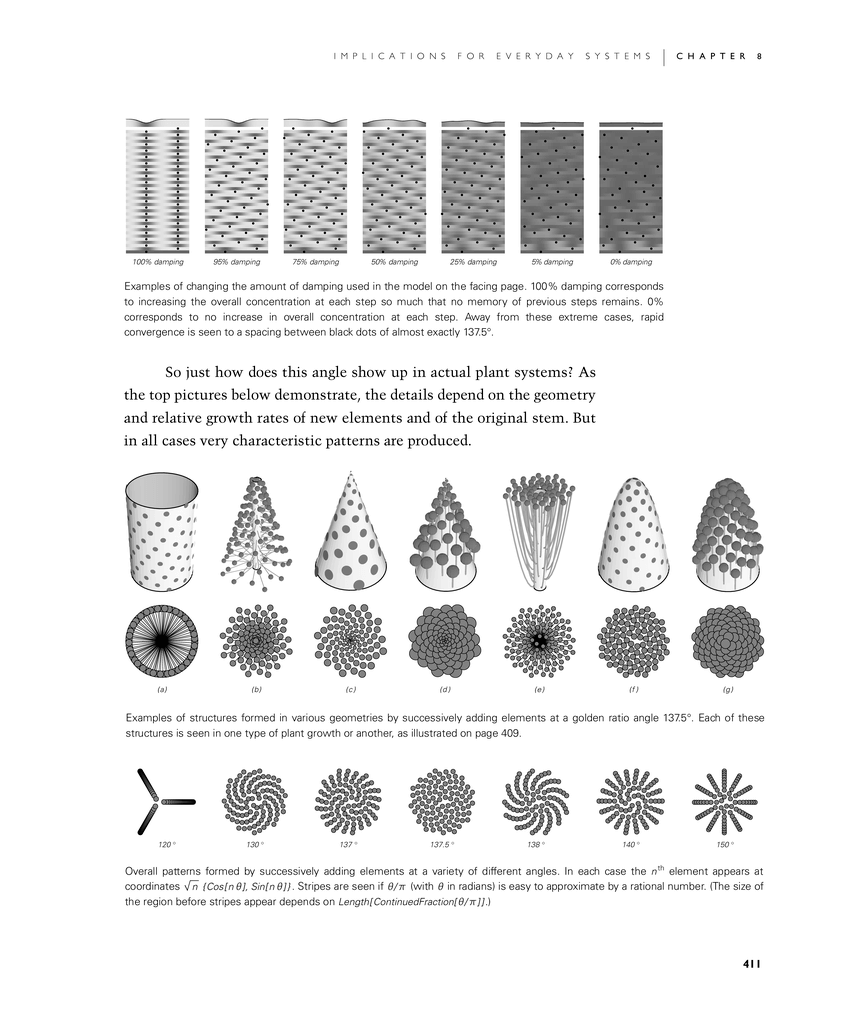
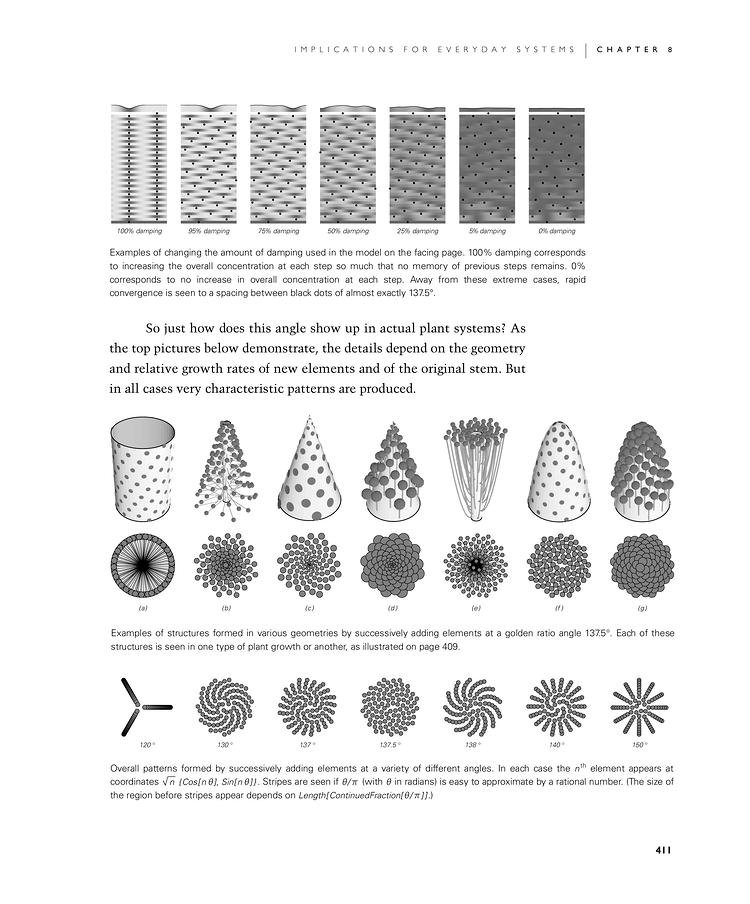
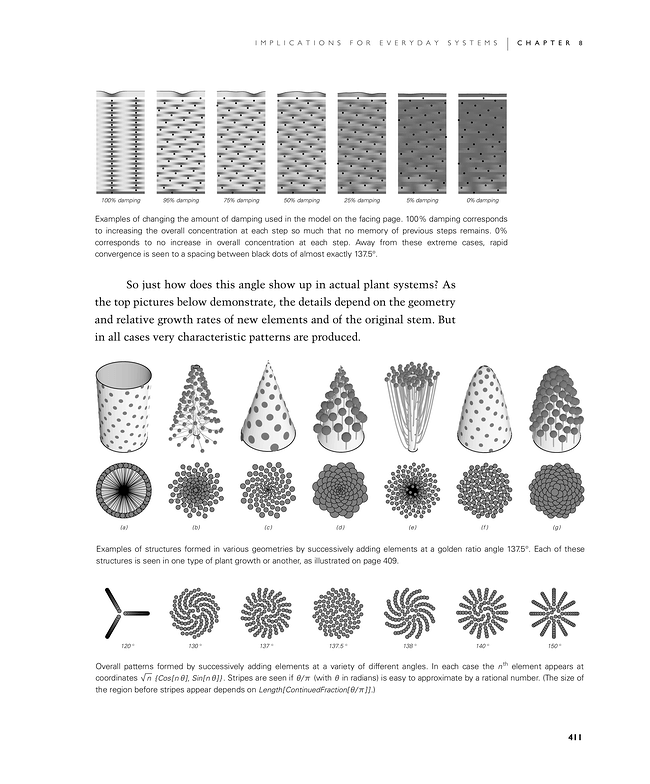
So just how does this angle show up in actual plant systems? As the top row of pictures in the second image below demonstrate, the details depend on the geometry and relative growth rates of new elements and of the original stem. But in all cases very characteristic patterns are produced.

Examples of changing the amount of damping used in the model on the facing page. 100% damping corresponds to increasing the overall concentration at each step so much that no memory of previous steps remains. 0% corresponds to no increase in overall concentration at each step. Away from these extreme cases, rapid convergence is seen to a spacing between black dots of almost exactly 137.5°.

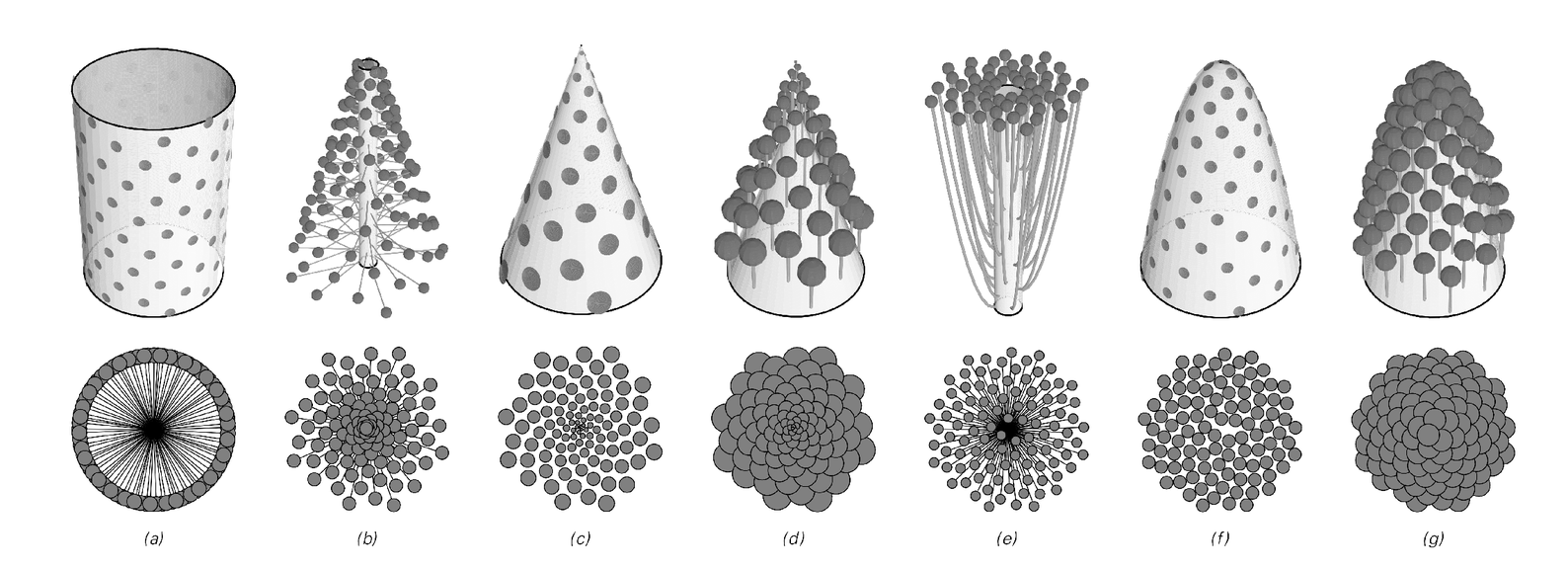
Examples of structures formed in various geometries by successively adding elements at a golden ratio angle 137.5°. Each of these structures is seen in one type of plant growth or another, as illustrated on page 409.

Overall patterns formed by successively adding elements at a variety of different angles. In each case the n^th element appears at coordinates Sqrt[n] {Cos[n θ],Sin[n θ]}. Stripes are seen if θ/π (with θ in radians) is easy to approximate by a rational number. (The size of the region before stripes appear depends on Length[ContinuedFraction[θ/π]].)