And given only the underlying rule for a substitution system, it turns out to be fairly difficult to tell even roughly what the spectrum will be like. But given the spectrum, one can immediately tell how we will perceive the sound. When the spectrum is dominated by just one large peak, we hear a definite tone. And when there are two large peaks we also typically hear definite tones. But as the number of peaks increases it rapidly becomes impossible to keep track of them, and we end up just hearing random noise—even in cases where the peaks happen to have frequencies that are in the ratios of common musical chords.
So the result is that our ears are not sensitive to most of the elaborate structure that we see in the spectra of many nested sequences. Indeed, it seems that as soon as the spectrum covers any broad range of frequencies all but very large peaks tend to be completely masked, just as in everyday life a sound needs to be loud if it is to be heard over background noise.
So what about other kinds of regularities in sequences? If a sequence is basically random but contains some short-range correlations then these will lead to smooth variations in the spectrum. And for example sequences that consist of random successions of specific blocks can yield any of the types of spectra shown below—and can sound variously like hisses, growls or gurgles.
To get a spectrum with a more elaborate structure requires long-range correlations—as exist in nested sequences. But so far as I can
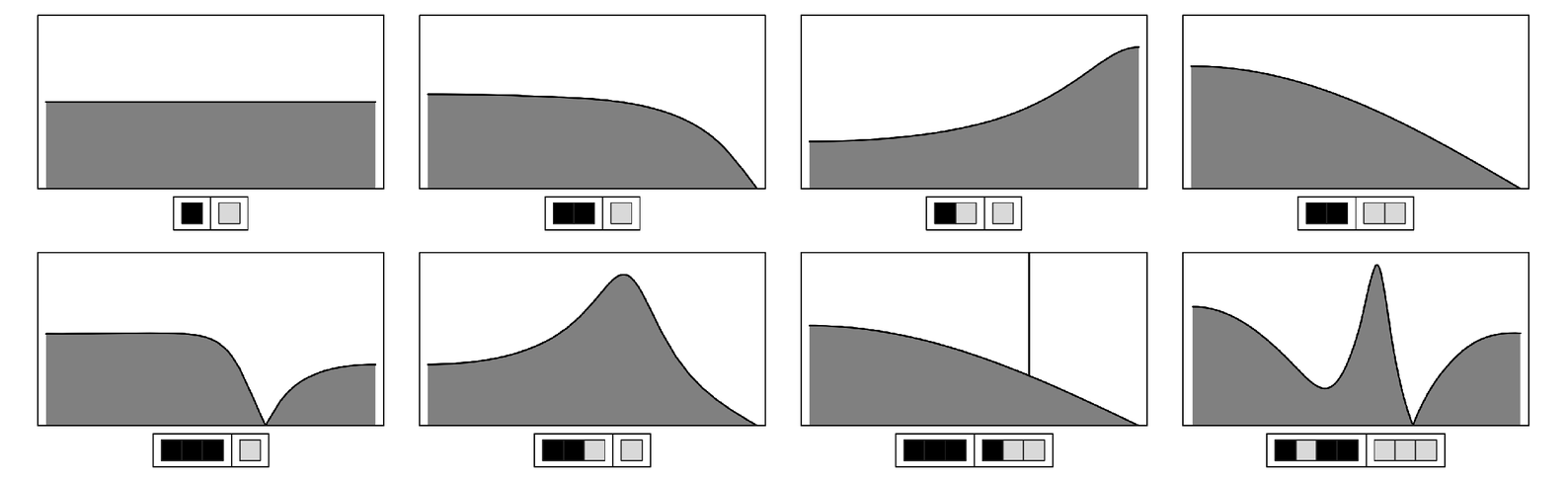
Frequency spectra for long sequences obtained by concatenating blocks in random orders. Such spectra can be calculated by fairly standard methods from stochastic analysis. The first case shown corresponds to white noise. The second-to-last case always has a black element at every third position, so exhibits a peak at the corresponding repetition frequency.



