that after going through perhaps nine trillion Turing machines one will definitely tend to find an example that is universal. But presumably one will actually find examples much earlier—since for example the 2-state 3-color machine on page 709 is only number 596,440.
And although these numbers are larger than for cellular automata, the fact remains that the simplest potentially universal Turing machines are still very simple in structure, suggesting that the threshold for universality in Turing machines—just like in cellular automata—is in many respects very low.
So what about other types of systems?
I suspect that in almost any case where we have seen complex behavior earlier in this book it will eventually be possible to show that there is universality. And indeed, as I will discuss at length in the next chapter, I believe that in general there is a close connection between universality and the appearance of complex behavior.
Previous examples of systems that are known to be universal have typically had rules that are far too complicated to see this with any clarity. But an almost unique instance where it could potentially have been seen even long ago are what are known as combinators.
Combinators are a particular case of the symbolic systems that we discussed on page 102 of Chapter 3. Originally intended as an idealized way to represent structures of functions defined in logic, combinators were actually first introduced in 1920—sixteen years before Turing machines. But although they have been investigated somewhat over the past eighty years, they have for the most part been viewed as rather obscure and irrelevant constructs.
The basic rules for combinators are given below.
With short initial conditions, the pictures at the top of the next page demonstrate that combinators tend to evolve quickly to simple fixed points. But with initial condition (e) of length 8 the pictures show
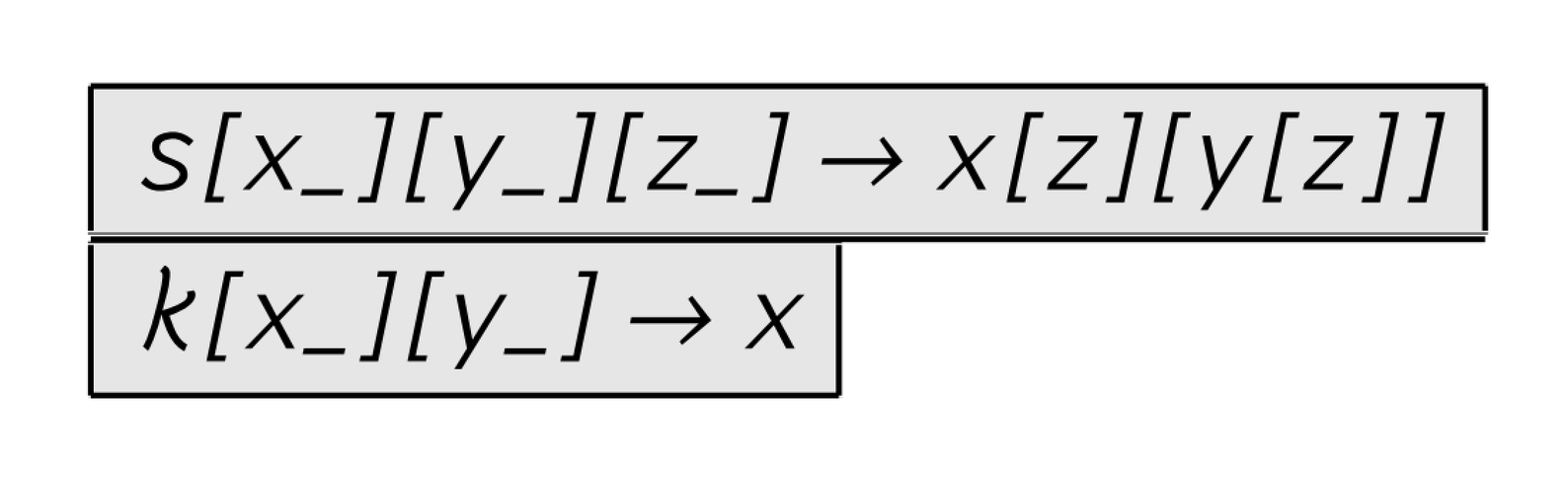
Rules for symbolic systems known as combinators, first introduced in 1920, and proved universal by the mid-1930s.



