cannot in general do is to find an easy theory that will tell one without much effort what every aspect of this behavior will be.
So given this, can theoretical science still be useful at all?
The answer is definitely yes. For even in its most traditional form it can often deal quite well with those aspects of behavior that happen to be simple enough to be computationally reducible. And since one can never know in advance how far computational reducibility will go in a particular system it is always worthwhile at least to try applying the traditional methods of theoretical science.
But ultimately if computational irreducibility is present then these methods will fail. Yet there are still often many reasons to want to use abstract theoretical models rather than just doing experiments on actual systems in nature and elsewhere. And as the results in this book suggest, by using the right kinds of models much can be achieved.
Any accurate model for a system that exhibits computational irreducibility must at some level inevitably involve computations that are as sophisticated as those in the system itself. But as I have shown in
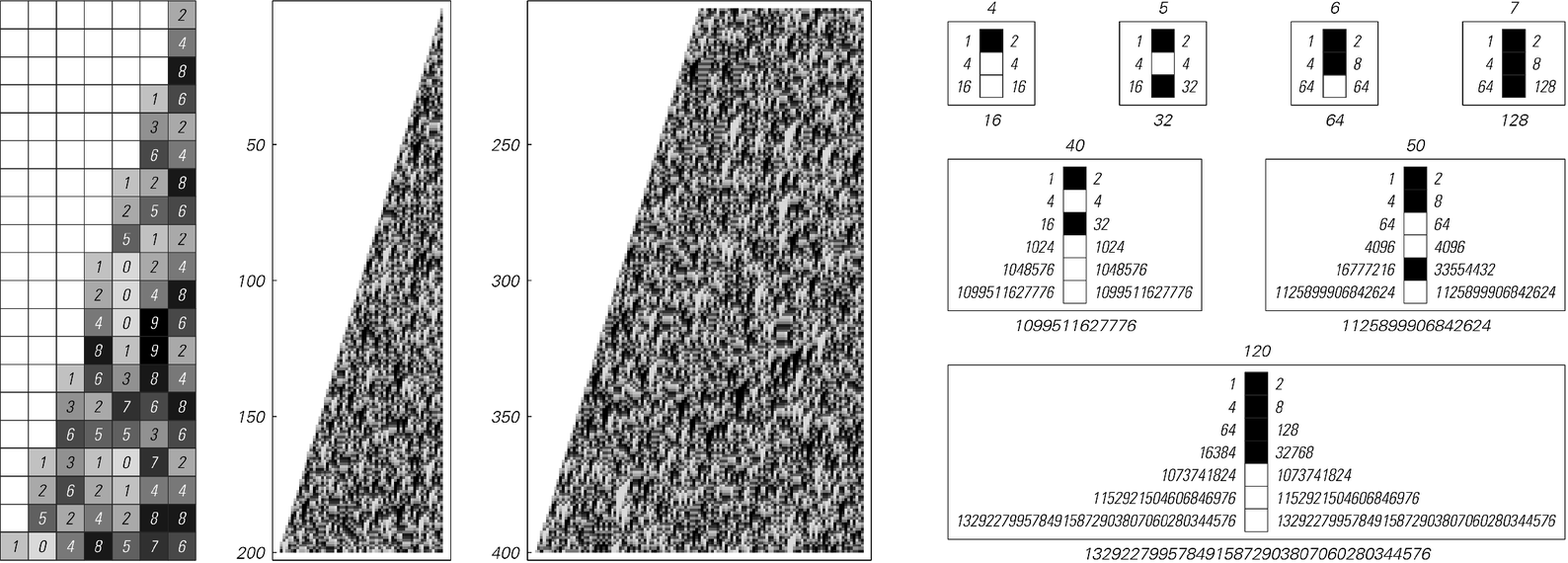
A system whose behavior looks complex but still turns out to be computationally reducible. The system is a cellular automaton with 10 possible colors for each cell. But it can also be viewed as a system based on numbers, in which successive rows are the base 10 digit sequences of successive powers of 2. And it turns out that there is a fast way to compute row n just from the base 2 digit sequence of n, as the pictures on the right illustrate. This procedure is based on the standard repeated squaring method of finding 2n by starting from 2, and then successively squaring the numbers one gets, multiplying by 2 if the corresponding base 2 digit in n is 1. Using this procedure one can certainly compute the color of any cell on row n by doing about n Log[n]3 operations—instead of the n2 needed if one carried out the cellular automaton evolution explicitly.



