Notes
Chapter 8: Implications for Everyday Systems
Section 1: Issues of Modelling https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-1--issues-of-modelling
https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-1--issues-of-modelling
Section 2: The Growth of Crystals https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-2--the-growth-of-crystals
https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-2--the-growth-of-crystals
Implementation [of hexagonal cellular automata]
Other models [of crystal growth]
Section 3: The Breaking of Materials https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-3--the-breaking-of-materials
https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-3--the-breaking-of-materials
Phenomenology of microscopic fracture
Models of microscopic fracture
Experimental data [on fracture]
Alternate models [of fracture]
Section 4: Fluid Flow https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-4--fluid-flow
https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-4--fluid-flow
Section 5: Fundamental Issues in Biology https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-5--fundamental-issues-in-biology
https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-5--fundamental-issues-in-biology
History [of biological complexity]
Tricks in [biological] evolution
Belief in [biological] optimality
Section 6: Growth of Plants and Animals https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-6--growth-of-plants-and-animals
https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-6--growth-of-plants-and-animals
History [of theories of biological form]
Implementation [of branching model]
Mathematical properties [of branching model]
Simple geometries [in branching model]
Projections of [phyllotaxis] patterns
Implementation [of phyllotaxis model]
Symmetries [in biological systems]
Discrete folding [in biological growth]
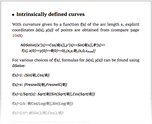
Multidimensional generalizations [of intrinsically defined curves]
Parametrizations of [biological] growth
Section 7: Biological Pigmentation Patterns https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-7--biological-pigmentation-patterns
https://www.wolframscience.com/nks/chap-8--implications-for-everyday-systems--notes#sect-8-7--biological-pigmentation-patterns
Animals [with patterning] shown
Implementation [of patterning model]
Features of the [patterning] model
Scales of patterns [on animals]







![Finding models [of systems] Finding models [of systems]](/nks/img/thumbnails/notes-8-1--finding-models-of-systems--textonly.png)


![Nucleation [of crystals] Nucleation [of crystals]](/nks/img/thumbnails/notes-8-2--nucleation-of-crystals--textonly.png)
![Implementation [of hexagonal cellular automata] Implementation [of hexagonal cellular automata]](/nks/img/thumbnails/notes-8-2--implementation-of-hexagonal-cellular-automata--textonly.png)





![Other models [of crystal growth] Other models [of crystal growth]](/nks/img/thumbnails/notes-8-2--other-models-of-crystal-growth--textonly.png)







![History [of fracture] History [of fracture]](/nks/img/thumbnails/notes-8-3--history-of-fracture--textonly.png)
![Experimental data [on fracture] Experimental data [on fracture]](/nks/img/thumbnails/notes-8-3--experimental-data-on-fracture--textonly.png)

![Alternate models [of fracture] Alternate models [of fracture]](/nks/img/thumbnails/notes-8-3--alternate-models-of-fracture--textonly.png)

![Crushing [of solids] Crushing [of solids]](/nks/img/thumbnails/notes-8-3--crushing-of-solids--textonly.png)




















![History [of biological complexity] History [of biological complexity]](/nks/img/thumbnails/notes-8-5--history-of-biological-complexity--textonly.png)

![Genetic programs [in biology] Genetic programs [in biology]](/nks/img/thumbnails/notes-8-5--genetic-programs-in-biology--textonly.png)
![Tricks in [biological] evolution Tricks in [biological] evolution](/nks/img/thumbnails/notes-8-5--tricks-in-biological-evolution--textonly.png)
![Belief in [biological] optimality Belief in [biological] optimality](/nks/img/thumbnails/notes-8-5--belief-in-biological-optimality--textonly.png)

![Other models [of mutation] Other models [of mutation]](/nks/img/thumbnails/notes-8-5--other-models-of-mutation--textonly.png)


![Smooth variables [in biology] Smooth variables [in biology]](/nks/img/thumbnails/notes-8-5--smooth-variables-in-biology--textonly.png)
![[Biological] species [Biological] species](/nks/img/thumbnails/notes-8-5--biological-species--textonly.png)

![Major new features [in biological evolution] Major new features [in biological evolution]](/nks/img/thumbnails/notes-8-5--major-new-features-in-biological-evolution--textonly.png)
![Software [system] statistics Software [system] statistics](/nks/img/thumbnails/notes-8-5--software-system-statistics--textonly.png)

![History [of theories of biological form] History [of theories of biological form]](/nks/img/thumbnails/notes-8-6--history-of-theories-of-biological-form--textonly.png)


![Implementation [of branching model] Implementation [of branching model]](/nks/img/thumbnails/notes-8-6--implementation-of-branching-model--textonly.png)
![Mathematical properties [of branching model] Mathematical properties [of branching model]](/nks/img/thumbnails/notes-8-6--mathematical-properties-of-branching-model--textonly.png)
![Simple geometries [in branching model] Simple geometries [in branching model]](/nks/img/thumbnails/notes-8-6--simple-geometries-in-branching-model--textonly.png)







![Projections of [phyllotaxis] patterns Projections of [phyllotaxis] patterns](/nks/img/thumbnails/notes-8-6--projections-of-phyllotaxis-patterns--textonly.png)
![Implementation [of phyllotaxis model] Implementation [of phyllotaxis model]](/nks/img/thumbnails/notes-8-6--implementation-of-phyllotaxis-model--textonly.png)
![Shapes of [biological] cells Shapes of [biological] cells](/nks/img/thumbnails/notes-8-6--shapes-of-biological-cells--textonly.png)
![Symmetries [in biological systems] Symmetries [in biological systems]](/nks/img/thumbnails/notes-8-6--symmetries-in-biological-systems--textonly.png)



![[Mollusc] shells [Mollusc] shells](/nks/img/thumbnails/notes-8-6--mollusc-shells--textonly.png)
![[Mollusc] shell model [Mollusc] shell model](/nks/img/thumbnails/notes-8-6--mollusc-shell-model--textonly.png)
![History [of shell models] History [of shell models]](/nks/img/thumbnails/notes-8-6--history-of-shell-models--textonly.png)
![Discrete folding [in biological growth] Discrete folding [in biological growth]](/nks/img/thumbnails/notes-8-6--discrete-folding-in-biological-growth--textonly.png)
![Multidimensional generalizations [of intrinsically defined curves] Multidimensional generalizations [of intrinsically defined curves]](/nks/img/thumbnails/notes-8-6--multidimensional-generalizations-of-intrinsically-defined-curves--textonly.png)




![Parametrizations of [biological] growth Parametrizations of [biological] growth](/nks/img/thumbnails/notes-8-6--parametrizations-of-biological-growth--textonly.png)
![Schemes for [biological] growth Schemes for [biological] growth](/nks/img/thumbnails/notes-8-6--schemes-for-biological-growth--textonly.png)



![[Biological] self-assembly [Biological] self-assembly](/nks/img/thumbnails/notes-8-6--biological-self-assembly--textonly.png)




![History [of shell patterns] History [of shell patterns]](/nks/img/thumbnails/notes-8-7--history-of-shell-patterns--textonly.png)
![Animals [with patterning] shown Animals [with patterning] shown](/nks/img/thumbnails/notes-8-7--animals-with-patterning-shown--textonly.png)

![Implementation [of patterning model] Implementation [of patterning model]](/nks/img/thumbnails/notes-8-7--implementation-of-patterning-model--textonly.png)
![Features of the [patterning] model Features of the [patterning] model](/nks/img/thumbnails/notes-8-7--features-of-the-patterning-model--textonly.png)

![Scales of patterns [on animals] Scales of patterns [on animals]](/nks/img/thumbnails/notes-8-7--scales-of-patterns-on-animals--textonly.png)

![Examples [of reaction-diffusion] in chemistry Examples [of reaction-diffusion] in chemistry](/nks/img/thumbnails/notes-8-7--examples-of-reaction-diffusion-in-chemistry--textonly.png)

![Origins of randomness [in animal patterning] Origins of randomness [in animal patterning]](/nks/img/thumbnails/notes-8-7--origins-of-randomness-in-animal-patterning--textonly.png)









