Notes
Chapter 12: The Principle of Computational Equivalence
Section 1: Basic Framework
https://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-1--basic-framework
Section 2: Outline of the Principlehttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-2--outline-of-the-principle
![Note for mathematicians [about PCE]](/nks/img/thumbnails/notes-12-2--note-for-mathematicians-about-pce--textonly.png "Note for mathematicians [about PCE]")
![History [of PCE]](/nks/img/thumbnails/notes-12-2--history-of-pce--textonly.png "History [of PCE]")
![[History of] Church's Thesis](/nks/img/thumbnails/notes-12-2--history-of-churchs-thesis--textonly.png "[History of] Church's Thesis")
Section 3: The Content of the Principlehttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-3--the-content-of-the-principle
![Character of [general] principles [in science]](/nks/img/thumbnails/notes-12-3--character-of-general-principles-in-science--textonly.png "Character of [general] principles [in science]")
![Oracles [for universal systems]](/nks/img/thumbnails/notes-12-3--oracles-for-universal-systems--textonly.png "Oracles [for universal systems]")
![Initial conditions [as oracles]](/nks/img/thumbnails/notes-12-3--initial-conditions-as-oracles--textonly.png "Initial conditions [as oracles]")
![Criteria for universality [in systems]](/nks/img/thumbnails/notes-12-3--criteria-for-universality-in-systems--textonly.png "Criteria for universality [in systems]")
![Encodings [for universality]](/nks/img/thumbnails/notes-12-3--encodings-for-universality--textonly.png "Encodings [for universality]")
![History [of universal objects]](/nks/img/thumbnails/notes-12-3--history-of-universal-objects--textonly.png "History [of universal objects]")
![[Construction of] universal objects](/nks/img/thumbnails/notes-12-3--construction-of-universal-objects--textonly.png "[Construction of] universal objects")
![Block occurrences [in rule 30]](/nks/img/thumbnails/notes-12-3--block-occurrences-in-rule-30--textonly.png "Block occurrences [in rule 30]")
Character of [general] principles [in science]
Oracles [for universal systems]
Initial conditions [as oracles]
Criteria for universality [in systems]
History [of universal objects]
Section 4: The Validity of the Principlehttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-4--the-validity-of-the-principle
![Initial conditions [and continuity]](/nks/img/thumbnails/notes-12-4--initial-conditions-and-continuity--textonly.png "Initial conditions [and continuity]")
![[Universality in] equations](/nks/img/thumbnails/notes-12-4--universality-in-equations--textonly.png "[Universality in] equations")
![[Time compression in] ODEs](/nks/img/thumbnails/notes-12-4--time-compression-in-odes--textonly.png "[Time compression in] ODEs")
![Emulating discrete systems [with continuous ones]](/nks/img/thumbnails/notes-12-4--emulating-discrete-systems-with-continuous-ones--textonly.png "Emulating discrete systems [with continuous ones]")
![Human thinking [and PCE]](/nks/img/thumbnails/notes-12-4--human-thinking-and-pce--textonly.png "Human thinking [and PCE]")
Section 5: Explaining the Phenomenon of Complexityhttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-5--explaining-the-phenomenon-of-complexity
Section 6: Computational Irreducibilityhttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-6--computational-irreducibility
![History [of computational irreducibility]](/nks/img/thumbnails/notes-12-6--history-of-computational-irreducibility--textonly.png "History [of computational irreducibility]")
![[History of] exact solutions](/nks/img/thumbnails/notes-12-6--history-of-exact-solutions--textonly.png "[History of] exact solutions")
![Amount of computation [and computational irreducibility]](/nks/img/thumbnails/notes-12-6--amount-of-computation-and-computational-irreducibility--textonly.png "Amount of computation [and computational irreducibility]")
![More complicated rules [and reducibility]](/nks/img/thumbnails/notes-12-6--more-complicated-rules-and-reducibility--textonly.png "More complicated rules [and reducibility]")
![[Examples of] reducible systems](/nks/img/thumbnails/notes-12-6--examples-of-reducible-systems--textonly.png "[Examples of] reducible systems")
![[Computation of] mathematical functions](/nks/img/thumbnails/notes-12-6--computation-of-mathematical-functions--textonly.png "[Computation of] mathematical functions")
![Formulas [and computational irreducibility]](/nks/img/thumbnails/notes-12-6--formulas-and-computational-irreducibility--textonly.png "Formulas [and computational irreducibility]")
![[Examples of] short computations](/nks/img/thumbnails/notes-12-6--examples-of-short-computations--textonly.png "[Examples of] short computations")
History [of computational irreducibility]
Amount of computation [and computational irreducibility]
More complicated rules [and reducibility]
[Examples of] reducible systems
[Computation of] mathematical functions
Formulas [and computational irreducibility]
Section 7: The Phenomenon of Free Willhttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-7--the-phenomenon-of-free-will
![History [of ideas about free will]](/nks/img/thumbnails/notes-12-7--history-of-ideas-about-free-will--textonly.png "History [of ideas about free will]")
![Responsibility [and free will]](/nks/img/thumbnails/notes-12-7--responsibility-and-free-will--textonly.png "Responsibility [and free will]")
![[Free] will and purpose](/nks/img/thumbnails/notes-12-7--free-will-and-purpose--textonly.png "[Free] will and purpose")
![Source of [free] will](/nks/img/thumbnails/notes-12-7--source-of-free-will--textonly.png "Source of [free] will")
Section 8: Undecidability and Intractabilityhttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-8--undecidability-and-intractability
![History [of undecidability]](/nks/img/thumbnails/notes-12-8--history-of-undecidability--textonly.png "History [of undecidability]")
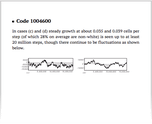
![[Undecidability in] natural systems](/nks/img/thumbnails/notes-12-8--undecidability-in-natural-systems--textonly.png "[Undecidability in] natural systems")
![[Classes of] fast algorithms](/nks/img/thumbnails/notes-12-8--classes-of-fast-algorithms--textonly.png "[Classes of] fast algorithms")
![History [of computational complexity theory]](/nks/img/thumbnails/notes-12-8--history-of-computational-complexity-theory--textonly.png "History [of computational complexity theory]")
![Lower bounds [on computational complexity]](/nks/img/thumbnails/notes-12-8--lower-bounds-on-computational-complexity--textonly.png "Lower bounds [on computational complexity]")
![[One-sided] Turing machines](/nks/img/thumbnails/notes-12-8--one-sided-turing-machines--textonly.png "[One-sided] Turing machines")
![Functions [computed by Turing machines]](/nks/img/thumbnails/notes-12-8--functions-computed-by-turing-machines--textonly.png "Functions [computed by Turing machines]")
![[Turing] machine 1507](/nks/img/thumbnails/notes-12-8--turing-machine-1507--textonly.png "[Turing] machine 1507")
![Properties [of example Turing machines]](/nks/img/thumbnails/notes-12-8--properties-of-example-turing-machines--textonly.png "Properties [of example Turing machines]")
![Longest halting times [in Turing machines]](/nks/img/thumbnails/notes-12-8--longest-halting-times-in-turing-machines--textonly.png "Longest halting times [in Turing machines]")
![Growth rates [of halting times]](/nks/img/thumbnails/notes-12-8--growth-rates-of-halting-times--textonly.png "Growth rates [of halting times]")
![[Turing] machine 600720](/nks/img/thumbnails/notes-12-8--turing-machine-600720--textonly.png "[Turing] machine 600720")
![[NP completeness in] natural systems](/nks/img/thumbnails/notes-12-8--np-completeness-in-natural-systems--textonly.png "[NP completeness in] natural systems")
![Implementation [of TM cellular automaton]](/nks/img/thumbnails/notes-12-8--implementation-of-tm-cellular-automaton--textonly.png "Implementation [of TM cellular automaton]")
![Satisfiability [emulating Turing machines]](/nks/img/thumbnails/notes-12-8--satisfiability-emulating-turing-machines--textonly.png "Satisfiability [emulating Turing machines]")
![[Intractability in] systems of limited size](/nks/img/thumbnails/notes-12-8--intractability-in-systems-of-limited-size--textonly.png "[Intractability in] systems of limited size")
![[Computational complexity of] finding outcomes](/nks/img/thumbnails/notes-12-8--computational-complexity-of-finding-outcomes--textonly.png "[Computational complexity of] finding outcomes")
Undecidability in cellular automata
[Undecidability in] natural systems
Undecidability in tiling problems
Computational complexity theory
History [of computational complexity theory]
Lower bounds [on computational complexity]
Functions [computed by Turing machines]
Properties [of example Turing machines]
Longest halting times [in Turing machines]
Growth rates [of halting times]
[NP completeness in] natural systems
Non-deterministic Turing machines
Implementation [of TM cellular automaton]
Satisfiability [emulating Turing machines]
[Intractability in] systems of limited size
Section 9: Implications for Mathematics and Its Foundationshttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-9--implications-for-mathematics-and-its-foundations
![History [of concept of mathematics]](/nks/img/thumbnails/notes-12-9--history-of-concept-of-mathematics--textonly.png "History [of concept of mathematics]")
![[History of] models of mathematics](/nks/img/thumbnails/notes-12-9--history-of-models-of-mathematics--textonly.png "[History of] models of mathematics")
![Basic logic [and axioms]](/nks/img/thumbnails/notes-12-9--basic-logic-and-axioms--textonly.png "Basic logic [and axioms]")
![[Axioms for] arithmetic](/nks/img/thumbnails/notes-12-9--axioms-for-arithmetic--textonly.png "[Axioms for] arithmetic")
![Groups [and axioms]](/nks/img/thumbnails/notes-12-9--groups-and-axioms--textonly.png "Groups [and axioms]")
![Semigroups [and axioms]](/nks/img/thumbnails/notes-12-9--semigroups-and-axioms--textonly.png "Semigroups [and axioms]")
![Fields [and axioms]](/nks/img/thumbnails/notes-12-9--fields-and-axioms--textonly.png "Fields [and axioms]")
![Rings [and axioms]](/nks/img/thumbnails/notes-12-9--rings-and-axioms--textonly.png "Rings [and axioms]")
![Real algebra [and axioms]](/nks/img/thumbnails/notes-12-9--real-algebra-and-axioms--textonly.png "Real algebra [and axioms]")
![[Axioms for] geometry](/nks/img/thumbnails/notes-12-9--axioms-for-geometry--textonly.png "[Axioms for] geometry")
![Set theory [and axioms]](/nks/img/thumbnails/notes-12-9--set-theory-and-axioms--textonly.png "Set theory [and axioms]")
![General topology [and axioms]](/nks/img/thumbnails/notes-12-9--general-topology-and-axioms--textonly.png "General topology [and axioms]")
![[Axioms for] real analysis](/nks/img/thumbnails/notes-12-9--axioms-for-real-analysis--textonly.png "[Axioms for] real analysis")
![Implementation [of proof example]](/nks/img/thumbnails/notes-12-9--implementation-of-proof-example--textonly.png "Implementation [of proof example]")
![Substitution strategies [in proofs]](/nks/img/thumbnails/notes-12-9--substitution-strategies-in-proofs--textonly.png "Substitution strategies [in proofs]")
![One-way transformations [as axioms]](/nks/img/thumbnails/notes-12-9--one-way-transformations-as-axioms--textonly.png "One-way transformations [as axioms]")
![Reducing axiom [system] details](/nks/img/thumbnails/notes-12-9--reducing-axiom-system-details--textonly.png "Reducing axiom [system] details")
![[Mathematical] proofs in practice](/nks/img/thumbnails/notes-12-9--mathematical-proofs-in-practice--textonly.png "[Mathematical] proofs in practice")
![Properties [of example multiway systems]](/nks/img/thumbnails/notes-12-9--properties-of-example-multiway-systems-1--textonly.png "Properties [of example multiway systems]")
![[Methods for] proof searching](/nks/img/thumbnails/notes-12-9--methods-for-proof-searching--textonly.png "[Methods for] proof searching")
![Truth and falsity [in formal systems]](/nks/img/thumbnails/notes-12-9--truth-and-falsity-in-formal-systems--textonly.png "Truth and falsity [in formal systems]")
![Properties [of example multiway systems]](/nks/img/thumbnails/notes-12-9--properties-of-example-multiway-systems-2--textonly.png "Properties [of example multiway systems]")
![Essential incompleteness [in axiom systems]](/nks/img/thumbnails/notes-12-9--essential-incompleteness-in-axiom-systems--textonly.png "Essential incompleteness [in axiom systems]")
![[Universality of] predicate logic](/nks/img/thumbnails/notes-12-9--universality-of-predicate-logic--textonly.png "[Universality of] predicate logic")
![[Universality of] algebraic axioms](/nks/img/thumbnails/notes-12-9--universality-of-algebraic-axioms--textonly.png "[Universality of] algebraic axioms")
![[Universality of] set theory](/nks/img/thumbnails/notes-12-9--universality-of-set-theory--textonly.png "[Universality of] set theory")
![Growth rates [of functions]](/nks/img/thumbnails/notes-12-9--growth-rates-of-functions--textonly.png "Growth rates [of functions]")
![[Examples of] unprovable statements](/nks/img/thumbnails/notes-12-9--examples-of-unprovable-statements--textonly.png "[Examples of] unprovable statements")
![Encodings of arithmetic [by different operations]](/nks/img/thumbnails/notes-12-9--encodings-of-arithmetic-by-different-operations--textonly.png "Encodings of arithmetic [by different operations]")
![[The concept of] infinity](/nks/img/thumbnails/notes-12-9--the-concept-of-infinity--textonly.png "[The concept of] infinity")
![Properties [of Diophantine equations]](/nks/img/thumbnails/notes-12-9--properties-of-diophantine-equations--textonly.png "Properties [of Diophantine equations]")
![Large solutions [to Diophantine equations]](/nks/img/thumbnails/notes-12-9--large-solutions-to-diophantine-equations--textonly.png "Large solutions [to Diophantine equations]")
![Nearby powers [and integer equations]](/nks/img/thumbnails/notes-12-9--nearby-powers-and-integer-equations--textonly.png "Nearby powers [and integer equations]")
![Unsolved problems [in number theory]](/nks/img/thumbnails/notes-12-9--unsolved-problems-in-number-theory--textonly.png "Unsolved problems [in number theory]")
![More powerful axioms [for mathematics]](/nks/img/thumbnails/notes-12-9--more-powerful-axioms-for-mathematics--textonly.png "More powerful axioms [for mathematics]")
![[Theorems about] practical programs](/nks/img/thumbnails/notes-12-9--theorems-about-practical-programs--textonly.png "[Theorems about] practical programs")
![Rules [for multiway systems examples]](/nks/img/thumbnails/notes-12-9--rules-for-multiway-systems-examples--textonly.png "Rules [for multiway systems examples]")
![Consistency [in axiom systems]](/nks/img/thumbnails/notes-12-9--consistency-in-axiom-systems--textonly.png "Consistency [in axiom systems]")
![Properties [of example multiway systems]](/nks/img/thumbnails/notes-12-9--properties-of-example-multiway-systems-3--textonly.png "Properties [of example multiway systems]")
![[Unprovable statements in] reduced arithmetic](/nks/img/thumbnails/notes-12-9--unprovable-statements-in-reduced-arithmetic--textonly.png "[Unprovable statements in] reduced arithmetic")
![Generators and relations [and axiom systems]](/nks/img/thumbnails/notes-12-9--generators-and-relations-and-axiom-systems--textonly.png "Generators and relations [and axiom systems]")
![[History of] truth tables](/nks/img/thumbnails/notes-12-9--history-of-truth-tables--textonly.png "[History of] truth tables")
![Implementation [of operators from axioms]](/nks/img/thumbnails/notes-12-9--implementation-of-operators-from-axioms--textonly.png "Implementation [of operators from axioms]")
![Properties [of operators from axioms]](/nks/img/thumbnails/notes-12-9--properties-of-operators-from-axioms--textonly.png "Properties [of operators from axioms]")
![Algebraic systems [and operator systems]](/nks/img/thumbnails/notes-12-9--algebraic-systems-and-operator-systems--textonly.png "Algebraic systems [and operator systems]")
![Symbolic systems [and operator systems]](/nks/img/thumbnails/notes-12-9--symbolic-systems-and-operator-systems--textonly.png "Symbolic systems [and operator systems]")
![Groups and semigroups [and operator systems]](/nks/img/thumbnails/notes-12-9--groups-and-semigroups-and-operator-systems--textonly.png "Groups and semigroups [and operator systems]")
![Forcing of operators [by axiom systems]](/nks/img/thumbnails/notes-12-9--forcing-of-operators-by-axiom-systems--textonly.png "Forcing of operators [by axiom systems]")
![Multiway systems [and operator systems]](/nks/img/thumbnails/notes-12-9--multiway-systems-and-operator-systems--textonly.png "Multiway systems [and operator systems]")
![Properties [of logical primitives]](/nks/img/thumbnails/notes-12-9--properties-of-logical-primitives--textonly.png "Properties [of logical primitives]")
![Notations [for logical primitives]](/nks/img/thumbnails/notes-12-9--notations-for-logical-primitives--textonly.png "Notations [for logical primitives]")
![Searching for logic [axioms]](/nks/img/thumbnails/notes-12-9--searching-for-logic-axioms--textonly.png "Searching for logic [axioms]")
![Two-operator logic [axioms]](/nks/img/thumbnails/notes-12-9--two-operator-logic-axioms--textonly.png "Two-operator logic [axioms]")
![History [of logic axioms]](/nks/img/thumbnails/notes-12-9--history-of-logic-axioms--textonly.png "History [of logic axioms]")
![Theorem distributions [in standard mathematics]](/nks/img/thumbnails/notes-12-9--theorem-distributions-in-standard-mathematics--textonly.png "Theorem distributions [in standard mathematics]")
![Ordering of [mathematical] constructs](/nks/img/thumbnails/notes-12-9--ordering-of-mathematical-constructs--textonly.png "Ordering of [mathematical] constructs")
![Frameworks [in mathematics]](/nks/img/thumbnails/notes-12-9--frameworks-in-mathematics--textonly.png "Frameworks [in mathematics]")
History [of concept of mathematics]
[History of] models of mathematics
Implementation [of proof example]
Substitution strategies [in proofs]
One-way transformations [as axioms]
Reducing axiom [system] details
[Mathematical] proofs in practice
Properties [of example multiway systems]
Truth and falsity [in formal systems]
Properties [of example multiway systems]
Essential incompleteness [in axiom systems]
[Universality of] predicate logic
[Universality of] algebraic axioms
Universal Diophantine equation
Statements in Peano arithmetic
[Examples of] unprovable statements
Encodings of arithmetic [by different operations]
Properties [of Diophantine equations]
Large solutions [to Diophantine equations]
Nearby powers [and integer equations]
Unsolved problems [in number theory]
More powerful axioms [for mathematics]
[Theorems about] practical programs
Rules [for multiway systems examples]
Consistency [in axiom systems]
Properties [of example multiway systems]
[Unprovable statements in] reduced arithmetic
Generators and relations [and axiom systems]
Comparison to multiway systems
Implementation [of operators from axioms]
Properties [of operators from axioms]
Algebraic systems [and operator systems]
Symbolic systems [and operator systems]
Groups and semigroups [and operator systems]
Forcing of operators [by axiom systems]
Multiway systems [and operator systems]
Properties [of logical primitives]
Notations [for logical primitives]
Theorem distributions [in standard mathematics]
Invention versus discovery in mathematics
Section 10: Intelligence in the Universehttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-10--intelligence-in-the-universe
![History [of extraterrestrial life]](/nks/img/thumbnails/notes-12-10--history-of-extraterrestrial-life--textonly.png "History [of extraterrestrial life]")
![[Ideas of] meaning in programs](/nks/img/thumbnails/notes-12-10--ideas-of-meaning-in-programs--textonly.png "[Ideas of] meaning in programs")
![Forms of [engineered] artifacts](/nks/img/thumbnails/notes-12-10--forms-of-engineered-artifacts--textonly.png "Forms of [engineered] artifacts")
![[Meaning in] molecular biology](/nks/img/thumbnails/notes-12-10--meaning-in-molecular-biology--textonly.png "[Meaning in] molecular biology")
![Possible purposes [for systems]](/nks/img/thumbnails/notes-12-10--possible-purposes-for-systems--textonly.png "Possible purposes [for systems]")
![Doubling rules [cellular automata]](/nks/img/thumbnails/notes-12-10--doubling-rules-cellular-automata--textonly.png "Doubling rules [cellular automata]")
![Searching [for doubling rules]](/nks/img/thumbnails/notes-12-10--searching-for-doubling-rules--textonly.png "Searching [for doubling rules]")
![Properties [of doubling rules]](/nks/img/thumbnails/notes-12-10--properties-of-doubling-rules--textonly.png "Properties [of doubling rules]")
![[Rules implementing] other functions](/nks/img/thumbnails/notes-12-10--rules-implementing-other-functions--textonly.png "[Rules implementing] other functions")
![Other examples [of minimal systems]](/nks/img/thumbnails/notes-12-10--other-examples-of-minimal-systems--textonly.png "Other examples [of minimal systems]")
![[History of] SETI](/nks/img/thumbnails/notes-12-10--history-of-seti--textonly.png "[History of] SETI")
![Detection methods [for SETI]](/nks/img/thumbnails/notes-12-10--detection-methods-for-seti--textonly.png "Detection methods [for SETI]")
![Messages to send [to extraterrestrials]](/nks/img/thumbnails/notes-12-10--messages-to-send-to-extraterrestrials--textonly.png "Messages to send [to extraterrestrials]")
![P versus NP [and messages]](/nks/img/thumbnails/notes-12-10--p-versus-np-and-messages--textonly.png "P versus NP [and messages]")
![Science fiction [and extraterrestrials]](/nks/img/thumbnails/notes-12-10--science-fiction-and-extraterrestrials--textonly.png "Science fiction [and extraterrestrials]")
![Practical arguments [about exterrestrials]](/nks/img/thumbnails/notes-12-10--practical-arguments-about-exterrestrials--textonly.png "Practical arguments [about exterrestrials]")
History [of extraterrestrial life]
[Ideas of] meaning in programs
Forms of [engineered] artifacts
[Meaning in] molecular biology
Possible purposes [for systems]
Doubling rules [cellular automata]
Searching [for doubling rules]
Properties [of doubling rules]
[Rules implementing] other functions
Minimal cellular automata for sequences
Other examples [of minimal systems]
Higher perception and analysis
Messages to send [to extraterrestrials]
Science fiction [and extraterrestrials]
Section 11: Implications for Technologyhttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-11--implications-for-technology
![Covering [implications for] technology](/nks/img/thumbnails/notes-12-11--covering-implications-for-technology--textonly.png "Covering [implications for] technology")
![[Implications for] chemistry](/nks/img/thumbnails/notes-12-11--implications-for-chemistry--textonly.png "[Implications for] chemistry")
Section 12: Historical Perspectiveshttps://www.wolframscience.com/nks/chap-12--the-principle-of-computational-equivalence--notes#sect-12-12--historical-perspectives
![Microcosm [and PCE]](/nks/img/thumbnails/notes-12-12--microcosm-and-pce--textonly.png "Microcosm [and PCE]")
